Transformer Phasing - The Dot Notation

  • 4K Views
  • Last Post 02 October 2018
Chris posted this 03 October 2017

The Dot Notation

Generally, when we study about Transformers, we assume that the primary and secondary voltage and currents are in phase. But, such is not always the case. In Transformer, The phase relation between primary and secondary currents and voltages depends on how each winding is wrapped around the core.

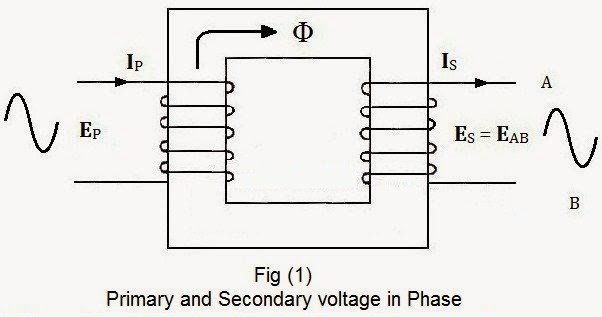
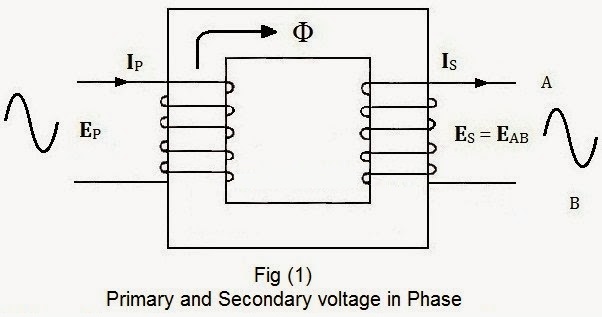
Refer to fig (1) and (2), you may see that the primary sides of both transformers are identical i.e. primary windings of both transformers wrapped in the same direction around the core.

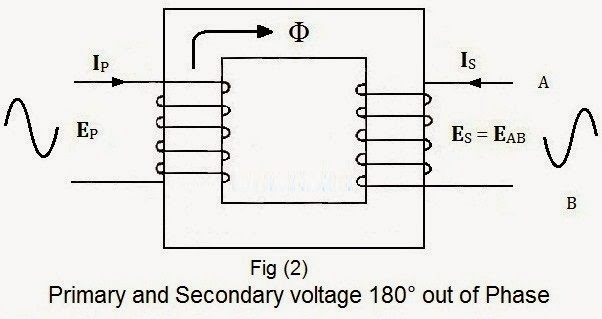
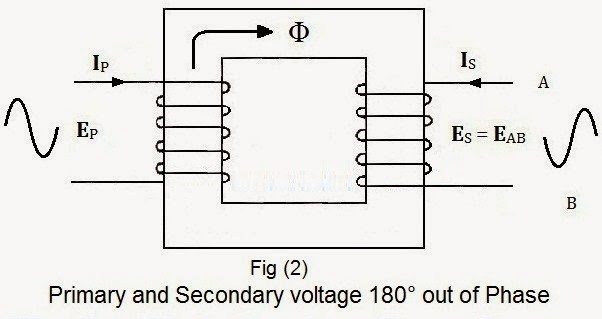
But in fig (2) you may notice that the secondary winding is wound around the core in the opposite direction from the secondary winding in fig (1).

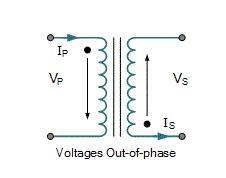
Consequently, the voltage induced in the Secondary winding in fig (2) is 180° out of phase as compared with the induced voltage in secondary in fig (1) and the direction of secondary current (IS) is opposite from the primary current (IP)

So we see that

  • The primary and secondary voltage and current are in phase in fig (1)
  • The primary and secondary voltage and current are 180° out of phase in fig (2)

 

Dot Convention

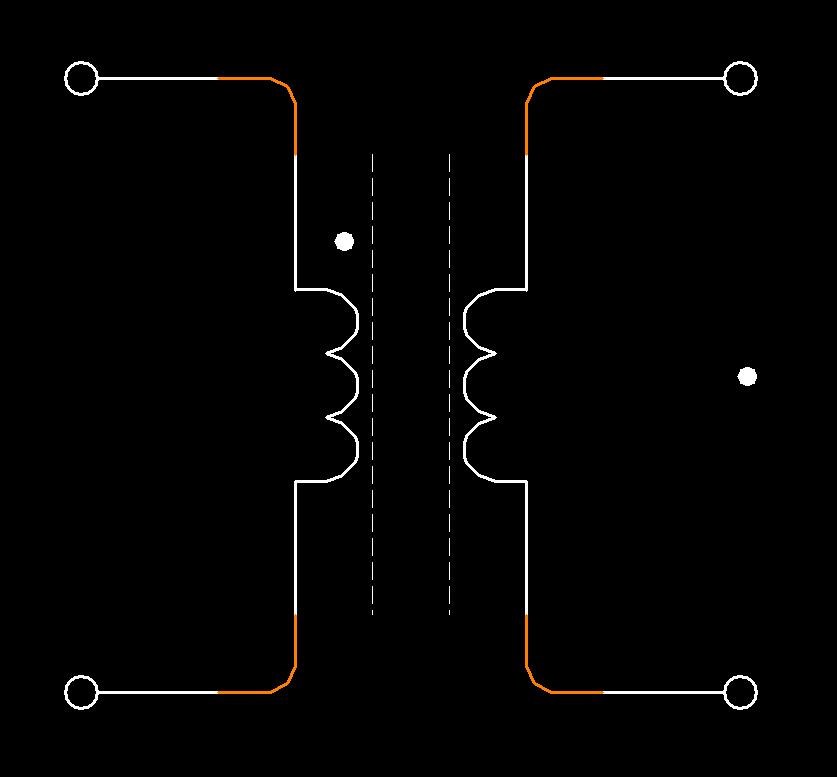
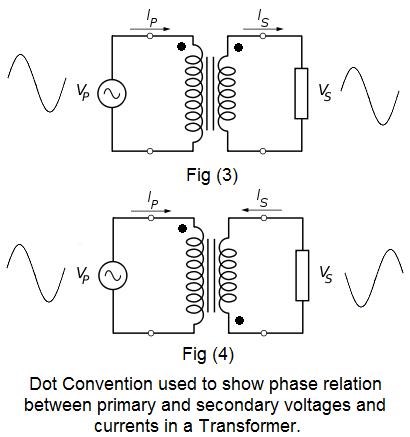
To eliminate any confusion in the phase relation between primary and secondary voltage and current, a dot convention has been adopted for transformer schematic diagrams. Dots are placed on the top of primary and secondary terminals as shown in fig (3) and (4)

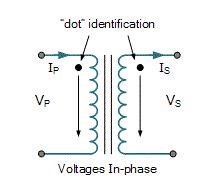
In fig (3), we see that dots are placed at the top in both primary and secondary terminals. It shows that the primary and secondary current and voltages are in phase. Moreover, the primary and secondary voltages (VP and VS) have similar sine wave, also the primary and secondary (IP and IS) currents are same in direction.

The story is opposite in fig (4). We can see that one dot is positioned at the top in primary terminal and the other one (dot) is placed at bottom of secondary terminal. It shows that the primary and secondary current and voltages are 180° out of phase. In addition, the primary and secondary voltages (VP and VS) sine waves are opposite to each other. Also the primary and secondary currents (IPand IS) are opposite in direction.

Please note: This article is in reference to: electricaltechnology.org

 

If Voltage and Currents are not in phase

For example, in an Autotransformer, we have Voltage in one polarity and Current in another. I want to quote Wikipedia:

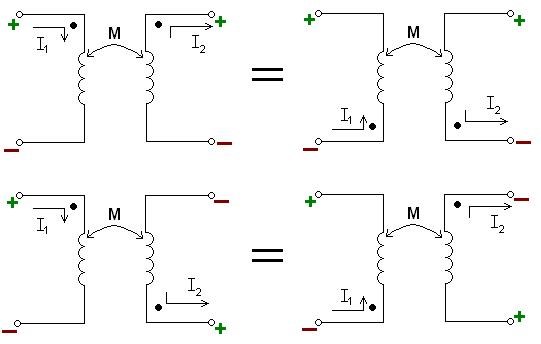
If two mutually coupled inductors are in series, the dot convention can be used in the same manner as in the case of autotransformers. Relative polarity in autotransformer drawings is usually quite obvious by physical placement of the windings in circuit drawings.

Autotransformers

 So we see that the Mutual Inductance is the determining factor but layout is important to take into account.

 

   Chris

 

EDIT:

Re-reading the Thread, I see my wording is not very good! I tried to point out the Dot Notation but in doing so, have made what I see now as confusing statements!

I apologise for this everyone!

Conventional Electromagnetic Induction is always Equal and Opposite minus Losses!

 

This is Fact and cant be disputed!

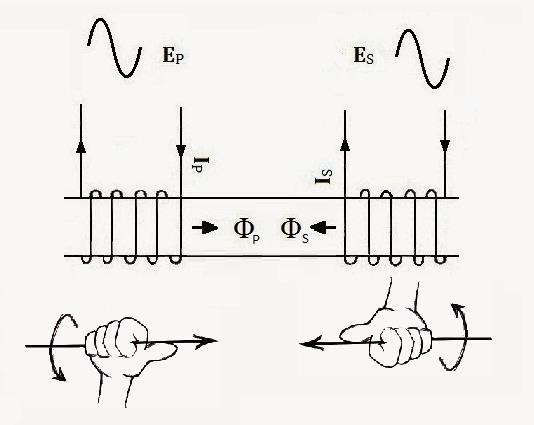
To make sense of this Thread, One must apply the Right Hand Grip Rule to the Coils.

Order By: Standard | Newest | Votes
Atti posted this 08 October 2017

Hi everybody!

I can approve the transformer experiments in the topic only. The flux change of the load is with an effect onto the original arrangement.See it here:  

Excuse me if cannot be understood,but I use web translation.

  • Liked by
  • Chris
Chris posted this 08 October 2017

Hi Vasile, Electromagnetic Induction, Mutual, Self Induction or any other type of Induction, is always Equal and Opposite.

This never changes and the article above is not clear on that. When the article says: "Primary and Secondary Voltage and Current are 180° out of phase" after saying: "Primary and Secondary Voltage and Current are in phase" is confusing at best.

This is however in the context of Winding Direction. Not Induction.

I try to think of the Dot Notation in terms of Voltage and Current Direction, but also in terms of how it is Induced or Applied. Each being opposite. An applied Voltage, and there for Current, will be opposite to an Induced Voltage and Current. This is Lenz's Law, equal and Opposite.

   Chris

Chris posted this 08 October 2017

Hi Atti - An excellent demonstration! Thank you for sharing this with us!

This does show a lot, a huge amount of data when studied!

Your work reminds me of the excellent work done by: Melvin Cobb

Yes you're right, each Induced Current is equal and Opposite, showing how a single System can invoke Electromagnetic Induction more than once!

There is a Magnetic Field equilibrium, each Field will try to equalise, and a single System does not have to be Symmetrical, we want an Asymmetrical System, in your case you have Two Outputs for the price of One!

Excellent Work! Thanks again for sharing!

   Chris

Prometheus posted this 01 October 2018

Something is messed up in Fig. 1 and Fig. 2. The arrows denoting current flow are backward.

----------

The Dot Notation is placed arbitrarily for the primary coil to begin (ie: you can put it on either lead of the primary, since we're dealing with AC current here), and each secondary coil must have a dot on the lead which results in a current flow which results in the same direction of magnetic flow in the core.

----------

So in Fig. 1, they've already given us a magnetic flux flow direction (clockwise), which implies a current flow direction and thus a dot location.

Wrapping the fingers of our right hand around in the direction of current flow (into the top lead of the primary coil), that gives us a clockwise magnetic flux direction in the core. So we'll put our first dot on the top lead of the primary winding.

Now we use the RHR on the secondary. We know the direction of magnetic flux flow, so our thumb points the way (down, palm away from you), and we match our fingers to current flow. We find that current entering at A results in the same magnetic flow direction in the core. So we put the dot at the top lead of the secondary. This is a 'straight-dot' transformer.

So the arrow on the secondary of Fig. 1 is backward. Current flows into the top lead of the primary, and into the top lead of the secondary, at the same time.

----------

In Fig. 2, we do the same, and we also get our first dot at the top lead of the primary.

Then using the RHR again, we let our thumb point the way (since we already know the core's magnetic flux flow direction). In this case, when current enters the secondary at B, it gives the same magnetic flux flow direction in the core. So we place our dot at the bottom lead. This is a 'cross-dot' transformer.

So again, the arrow on the secondary of Fig. 2 is incorrect. Current flows into the top lead of the primary, and into the bottom lead of the secondary, at the same time.
----------
In Fig. 1, from the perspective of the magnetic flux flowing through the core, assume the flux flows through the core in a clockwise direction. The coil on the left will appear to the flux to wind counter-clockwise, whereas the coil on the right will appear to the flux to wind clockwise.

In Fig. 1, from the perspective of the magnetic flux flowing through the core, assume the flux flows through the core in a counter-clockwise direction. The coil on the left will appear to the flux to wind counter-clockwise, whereas the coil on the right will appear to the flux to wind clockwise.

In Fig. 2, from the perspective of the magnetic flux flowing through the core, assume the flux flows through the core in a clockwise direction. The coil on the left will appear to the flux to wind counter-clockwise, whereas the coil on the right will also appear to the flux to wind counter-clockwise.

In Fig. 2, from the perspective of the magnetic flux flowing through the core, assume the flux flows through the core in a counter-clockwise direction. The coil on the left will appear to the flux to wind counter-clockwise, whereas the coil on the right will also appear to the flux to wind counter-clockwise.

Thus it can be seen that magnetic induction through a transformer core is a reflection transform (just as the B field of a permanent magnet is a reflection transform of the A field {B=curl(A)}... in this case, we're providing the "A" field from the primary coil, which is transformed via reflection into a magnetic field, which flips the phase).

For coils wound in the same direction (from the perspective of the flux), the phase is flipped 180 degrees, so to get input and output back into phase, we must flip the wind direction of one of the coils.

If it helps to visualize it, straighten out Fig. 1 and Fig. 2 so the core is a straight line.

----------

https://electronicspani.com/dot-convention-inductor-in-series-and-parallel/

A1, B1 and C1 are all dotted together in this transformer (although A2, B2 and C2 could just as legitimately be dotted together).

  • Liked by
  • Vidura
Chris posted this 01 October 2018

Prometheus,

Either I don't quite understand some of your statements, or I am not sure I would agree with some of your statements.

 

 

  • From Zero to Peak Flux, the Secondary Flux will Oppose the Action and the Magnetic Vectors are in opposite Directions.



  • From Peak Flux to Zero Flux, the Secondary Flux will Oppose the Action and the Magnetic Vectors are in opposite Directions.

 

There is no time that the Flux of the Secondary Adds Vectorially, to the Flux of the Primary, this never ever happens, the equation is always Negative, it never changes:

E.M.F = -N dΦ / dt

 

Where the ( - ) Negative Sign is Lenz Law in the Electromagnetic Induction Equation, always 180 Degrees out of Phase.

Now, at any one point in time, the Current in the Primary has a Forced Direction, we are Applying a Voltage, thus the Direction of the Current is a forced Function of the Applied Voltage. Critically, the Voltage and therefore the resulting Current, as a result of a load placed on the Secondary, is Induced via Electromagnetic Induction.

The Voltage and therefore the Current will always Oppose the Primary!

 

The Right Hand Grip Rule will always get you out of a jam! Fingers in the Direction of the Current, Thumb in the Direction of the North Pole.

NOTE: The above image as is Prometheus has suggested, it is of Fig 1, above as was questioned.

   Chris

Prometheus posted this 01 October 2018

You're talking about the bEMF, not the winding Dot Notation. The Dot Notation is designed such that if you were to apply voltage to any of the coils, you'd get the same magnetic flux direction in the core. This is important in multiple-secondary transformers. Forget about primary and secondary... there are some transformers which can have windings which act as primary sometimes, and secondary other times. Focus solely on magnetic flux direction.

You'll note the picture below just denotes magnetic flux (Φ), not Φpri and Φsec. There's a reason for that... the Dot Notation isn't looking at bEMF, merely at the direction of current flow in each coil which would give the same direction magnetic flux flow in the core.

This picture is Fig. 1 put into Paint and rotated so the coils are inline. Arrow direction hasn't been changed on the primary, the secondary arrow has been corrected.

Using the RHR, we can see that if current flows into the bottom lead of the primary (which, if flipped, would be the top lead in the Fig. 1 picture above), it gives a magnetic flux direction of downward. Using the same RHR, we can see that if current flows into the top lead of the secondary, it gives the same downward magnetic flux direction.

  • Liked by
  • Chris
Chris posted this 01 October 2018

Prometheus,

The direction of Current on the Secondary is not Correct.

 

 

Fig 1, the Current is in the other Direction!

We must not forget Induced Voltages, and therefore Currents are not the same as when we apply a Voltage and have a Load Current flowing.

   Chris

 

EDIT: I understand what you're saying, but, I have never read this rule, in-fact I have only ever read and seen Primary to Secondary Mutual Coupling that apply to the Dot Notation.

One example: http://gn.dronacharya.info/apsDept/Downloads/question_papers/ISem/Electrical-Engg/unit-4/Mutual_coupling_dotconvention.pdf

 

Prometheus posted this 01 October 2018

https://www.scribd.com/document/93588459/Transformer-Dot-Notation

Dot convention is used in order to indicate the phase relationship of the coils. Dots are placed beside each coil so that if currents are entering both dotted terminals or leaving both dotted terminals, the mutual fluxes produced by these currents will reinforce (add) with each other.

https://electronicspani.com/dot-convention-inductor-in-series-and-parallel/

Once the dot is placed on one coil, dots on the terminals of other remaining coils cannot be placed arbitrarily now.

Dots on other coils are now automatically decided according to the sense of the winding. Now we are to determine the position of dots on the terminals of the remaining windings corresponding to the dot placed at one of the terminals of winding A, which is at A1. Dot on the other winding is placed on such a terminal that a current entering through the dotted terminal magnetizes the core in the same direction as the flux created by current entering the dot on the first coil A.

It matters not which coil is primary and which is secondary... you can start by adding a dot arbitrarily to any lead of any coil... the rest of the dots must be placed such that that coil's winding direction and current flow constructively add to the magnetic flux flow in the core as delineated by the first-placed dot.

The Dot Notation is solely about the phase relationship of the coils.

  • Liked by
  • Chris
Chris posted this 01 October 2018

Thank you for the Links and quotes!

Well, no offense, but this is JP Morgan Sponsored Rule Set for sure!

No wonder so many Electrical Engineers I have spoken to, do not know Primary to Secondary Fluxes Oppose in a working Transformer! I have had one tell me that they don't, and that they Add.

Thee you have it, I stand corrected, and I guess we now see why so much confusion has been placed into the Dot Notion! Even I did not have it correct.

   Chris

 

 

Prometheus posted this 01 October 2018

Don't feel bad... even the falstad.com circuit emulator has it backward.

You'll note that in my re-aligned Fig. 1, the windings give the same phase relationship where the red dots are. That's all the Dot Notation is about... the phase relationship of the windings.

  • Liked by
  • Chris
  • Vidura
Chris posted this 01 October 2018

A Correction is required:

Credit to Prometheus, and for correctness, we must take this into account:

Apologies all, my research let my belief into the Mutual Coupling of the Coils as the Dot Notation. I hope this serves as a reminder and also why I say now and again, that I am not always right, I just try to share what I have learnt.

Please always cross reference, always more to learn!

   Chris

  • Liked by
  • Vidura
Prometheus posted this 02 October 2018

It should, however, be noted that Chris is correct as regards current flow when the transformer is in operation... but for the Dot Notation, we don't look at that, we merely look at what direction current flow in each coil will get us the same direction magnetic flux flow in the core, because that's what we need to know to determine which leads of each coil are going to be in-phase.

So for determining current flow, you'd use the RHR (Right Hand Generator Rule) to get the flow of magnetic flux in the core based upon the winding direction of the primary. Then you'd use the LHR (Left Hand Motor Rule) on the secondary (with your thumb pointing in the direction of the magnetic flux flow) to determine current flow direction during operation of the transformer.

And in this case, the current would flow into the top lead of the primary in Fig. 1, and out the top lead of the secondary.

  • Liked by
  • Chris
Jagau posted this 02 October 2018

The interpretation of the conventions in electricity is very subtle and as we can not see the magnetic field we must establish conventions. So for a transformer we use the dot convention.

It should be remembered that it is the primary voltage that produces a magnetic field which in turn produces a magnetic flux.

At the secondary level, this magnetic flux experienced by the primary produces a magnetic field. Thus, a voltage is produced which produces a current.

And for the direction of the current :


Here we have a transformer shows its two “dots” side by side on the two windings.

The current leaving the secondary dot is “in-phase” with the current entering the primary side dot.
Thus the polarities of the voltages at the dotted ends are also in-phase so when the voltage is positive at the dotted end of the primary coil, the voltage across the secondary coil is also positive at the dotted end.

 

The second transformer shows the two dots at opposite ends of the windings which means that the transformers primary and secondary coil windings are wound in opposite directions. The result of this is that the current leaving the secondary dot is 180o “out-of-phase” with the current entering the primary dot. The polarities of the voltages at the dotted ends are also out-of-phase so when the voltage is positive at the dotted end of the primary coil, the voltage across the corresponding secondary coil will be negative. Dont forget the sign plus ans less, so Chris in your first figure1 and figure2 you were right.


Jagau

  • Liked by
  • Chris
  • Aetherholic
Vidura posted this 02 October 2018

When i was thinking about the dot notations i found another inconsistency in this convenience, if the dot notation referes for the fasing of CURRENT flowing, in the case of reactive power it would be indefinite,as the currents are shifted at 90°including with the transformer loaded in some experiments. Only applying it to the voltage this would make sense.

  • Liked by
  • Jagau
  • Chris
Chris posted this 02 October 2018

Hey Vidura,

Good point! The solution is to put the Dot Notation out to the side like so:

 

No, I am sorry my friend, this is a terrible joke, I am making fun of the silly rules we are subjected to undecided

   Chris

We're Light Years Ahead!
Our Above Unity Machines:

Asymmetrical EMI

Wistiti's Bucking Joule Thief
Non-Inductive Coil Experiment
CD's Non-Inductive Coil Rep
Baerndorfer's Experiment
Captainloz's A-R-E
Aetherholic's COP>4.0

Resonant EMI

Yo's Ferro Resonance
Jagau's Non-linear Resonance
Ferrite at work
Recomended Protocol:
Measurement
Switching System
Measurement Block
Current Observation
Current Sensing Resolution
Members Online:
What is a Scalar:

In physics, scalars are physical quantities that are unaffected by changes to a vector space basis. Scalars are often accompanied by units of measurement, as in "10 cm". Examples of scalar quantities are mass, distance, charge, volume, time, speed, and the magnitude of physical vectors in general.

You need to forget the Non-Sense that some spout with out knowing the actual Definition of the word Scalar! Some people talk absolute Bull Sh*t!

The pressure P in the formula P = pgh, pgh is a scalar that tells you the amount of this squashing force per unit area in a fluid.

A Scalar, having both direction and magnitude, can be anything! The Magnetic Field, a Charge moving, yet some Numb Nuts think it means Magic Science!

Start Here:
Help with using the Forum.
Message from God:

Hello my children. This is Yahweh, the one true Lord. You have found creation's secret. Now share it peacefully with the world.

Ref: Message from God written inside the Human Genome

God be in my head, and in my thinking.

God be in my eyes, and in my looking.

God be in my mouth, and in my speaking.

Oh, God be in my heart, and in my understanding.

Your Support:

More than anything else, your contributions to this forum are most important! We are trying to actively get all visitors involved, but we do only have a few main contributors, which are very much appreciated! If you would like to see more pages with more detailed experiments and answers, perhaps a contribution of another type maybe possible:

PayPal De-Platformed me!

They REFUSE to tell me why!

We now use Wise!

Donate
Use E-Mail: Chris at aboveunity.com

The content I am sharing is not only unique, but is changing the world as we know it! Please Support Us!

Thank You So Much!

Browse by Category:
Weeks High Earners:
The great Nikola Tesla:

Ere many generations pass, our machinery will be driven by a power obtainable at any point of the universe. This idea is not novel. Men have been led to it long ago by instinct or reason. It has been expressed in many ways, and in many places, in the history of old and new. We find it in the delightful myth of Antheus, who drives power from the earth; we find it among the subtle speculations of one of your splendid mathematicians, and in many hints and statements of thinkers of the present time. Throughout space there is energy. Is this energy static or kinetic? If static, our hopes are in vain; if kinetic - and this we know it is for certain - then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.

Experiments With Alternate Currents Of High Potential And High Frequency (February 1892).

Close