Non-Linear Inductance

  • Topic Is Sticky
  • 3K Views
  • Last Post 11 April 2022
  • Topic Is Solved
Chris posted this 23 November 2018

Inductance ( L ) is the Rate at which Amperes can flow through the Coil in Time, this is defined as:

L = di / dt

One Henry is where One Ampere transitions the Coil in One Second. With Back E.M.F: 

L = ε / di / dt

Where ε is the Back E.M.F, restricting the Current Flow, created by the change in Current  that produced the E.M.F.

 

Confused?

 

Keep reading:

The Impedance of a Coil is calculated: Impedance ( Z ) = Voltage ( V ) / Current ( I ) and is given in units of Ohms ( Ω ).

Complex Impedance has two components, real and imaginary. An example of this would be: Z = R +j X

Where:

  • DC Resistance ( R ) = Real Component.
  • Reactance ( X ) = Imaginary Component.
  • +j = Voltage Leading.
  • -j = Voltage Lagging.

All components are real components, observable Circuit conditions.

Reactance ( X ) is composed of both Capacitive Reactance ( XC ) and Inductive Reactance ( XL ). In an LC Tank Circuit, at Resonance, XC and XL are equal and are said to cancel each other out. Thus in the LC Tank Circuit, the Capacitors Charge ( Q = C / V ) transforms into Magnetic Field ( B = μnI ) at maximum efficiency, which is measured as Quality Factor ( Q ) = Reactance ( X ) / Resistance ( R ).

So, if Reactance ( X ) is very low, say: 0.00001, and Resistance ( R ) is very low, say: 1.0, then Quality Factor ( Q ) = 0.00001 / 1.0 = 0.00001

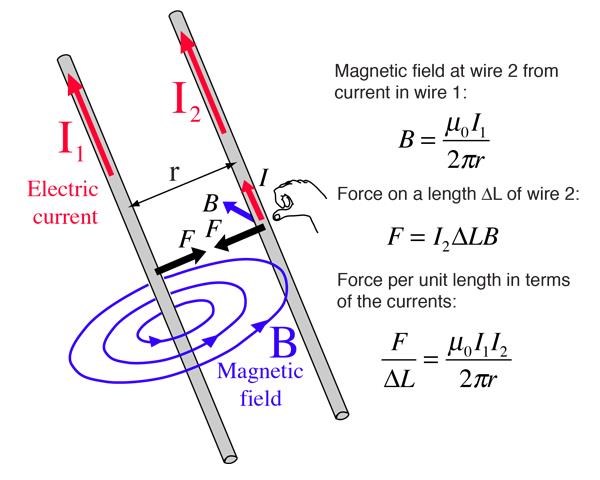
NOTE: Inductive Reactance ( XL ), is directly related to Faradays Law of Electromagnetic Induction!

 

 

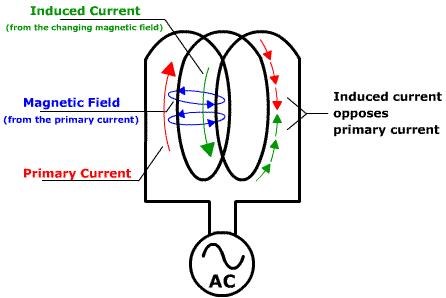
Faradays Law of Electromagnetic Induction: E.M.F = -N dPhi / dt, which is actually Back E.M.F, because of Self Induction inside the Coil, between the turns, this resists the Flow of Current, B.E.M.F = XL = ωL = 2pifL

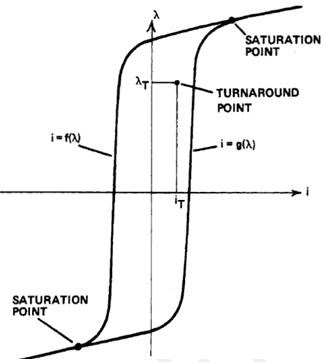
Also, remember, B and H are related in the following way:

 

 

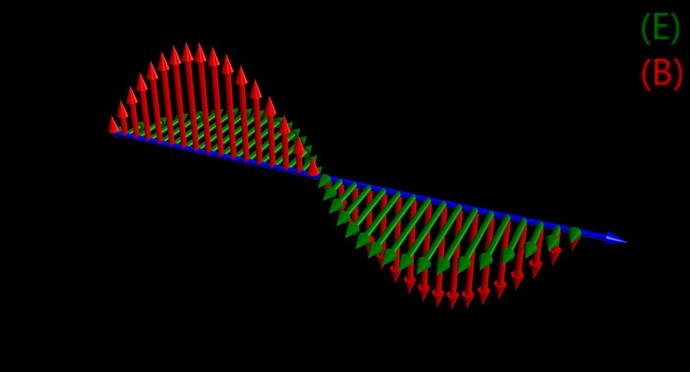
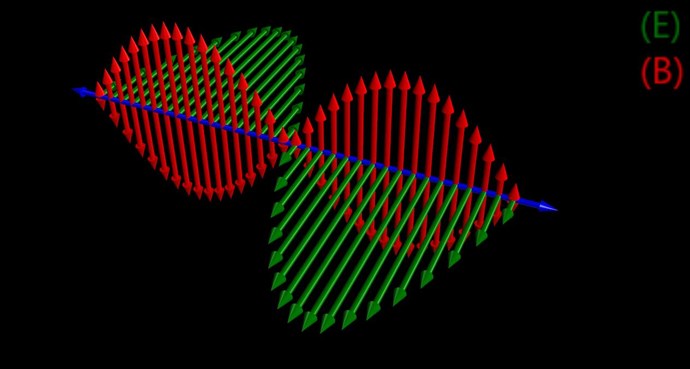
We know, the Cycle of the Transformation from Electric to Magnetic can be seen in Quadrants:

 

 

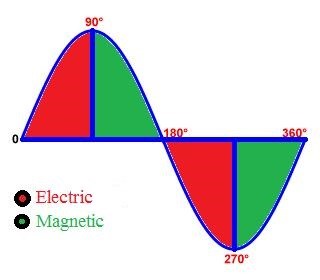
Red is Charge on the Capacitor ( Q = C / V ) charging the Inductor ( B = μnI ). At 90 degrees, the Capacitor has fully charged the Inductor, and the Inductor now Charges the Capacitor as the magnetic Field Changes in Time in the proximity of the Turns, yes Faradays law of Electromagnetic Induction again.

In an LC Tank Circuit, we see losses, Damping Factor ( ζ ) Zeta, and we see a typical decrease in the Amplitude of the Oscillations in an LC Tank Circuit:

 

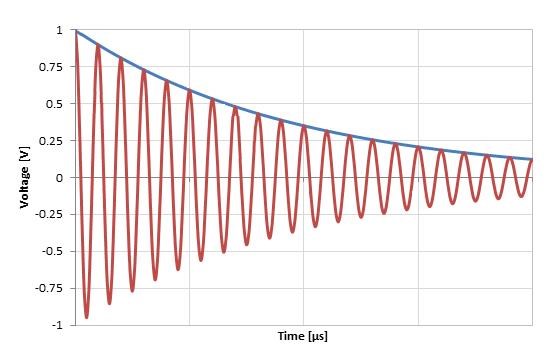
Inductance and Reactance all stay Linear, losses are not recoverable, and we see the Oscillations taper off.

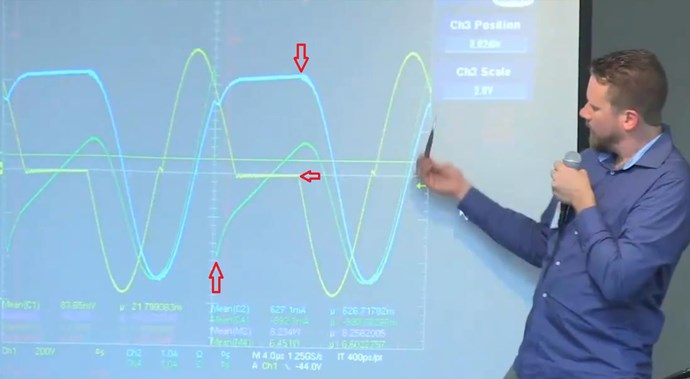
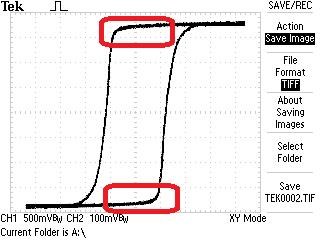
However, what is required to change, to Non-Linear Inductance? How can we see changes, enough to see a wave form like so:

 

 

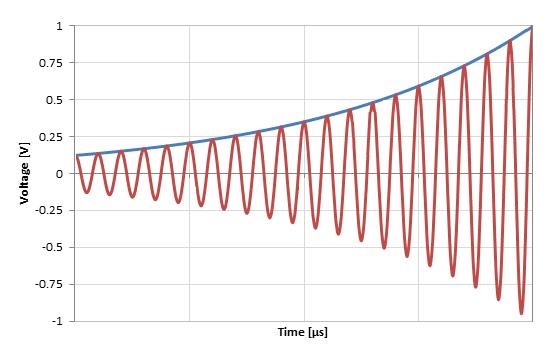
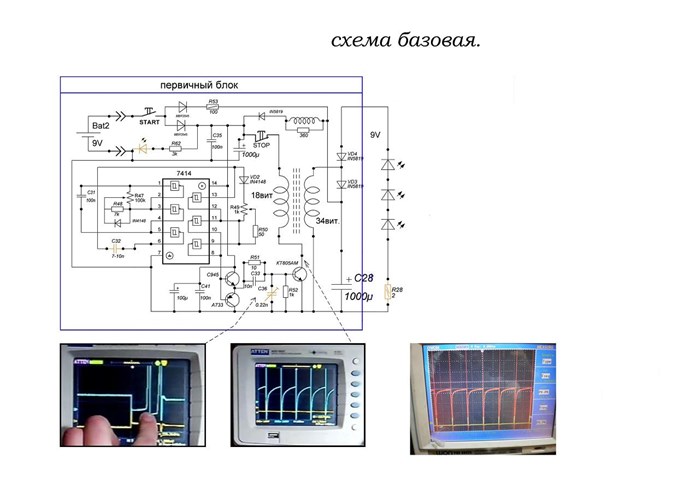
Knowing what we know, we must have any one of the above variables change. An experiment I have done, does show how this can be achieved: Reduced Impedance Effect

I do not agree entirely with Jim Murray. He has found a lot of what I have, his Transforming Generator does show the same effect as my Reduced Impedance Effect:

 

In the following video, if you listen carefully, Jim does say what I have, I = dL / dt:

 

So, it is possible, at 90 Degrees, we can change the Circuit, make the Circuit change, with The Reduced Impedance Effect, or other effects, to become more Re-Generative, or Less lossy.

But, please remember, we must not touch the Circuit between 0 and 90 degrees, and between 180 and 270, all Red Zones are No Go Zones!

By changing the Systems Inductance or any part of the Coils parameters, which in turn changes the Inductance, is a common theme we have seen a lot of.

The works of Don Smith, Floyd Sweet, Andrey Melnichenko, Clemente Figuera, and many others all take advantage of these effects.

Also similar to Zanzals Un-Named Device, also a Video Zanzal has shared:

 

This Technology is everywhere, its there for the taking, it only requires you understand these concepts and then apply them!

I think the term: Non-Linear Inductance is perhaps not entirely adequate for the description of what's actually going on. So I ask you, please think broadly about this and do not confine yourself to the specific of Inductance.

What is true, if we change the Rate at which Current can transition the Coil, we have also changed the Inductance!

Supporting Links:

 

   Chris

Order By: Standard | Newest | Votes
Atti posted this 23 November 2018

Hi.

One more thing I would like to add to the above.
Nonlinear energy storage elements may be:
1. capacitance diode, i.e. the capacity depends on the voltage applied
Rectangular iron core = nonlinear inductance ie inductance is a function of the current flowing through the coil. L (i)

This is a similar layout, but there is currently no secondary impulse here.

Other possible layouts.

http://001-lab.at.ua/publ/iz_seti/skhema_poljarizacii_kondensatorov/2-1-0-13

 

Jagau posted this 23 November 2018

To get a picture of what Chris said above, I would add this:


Resistance; is essentially friction against the motion of electrons =  express by R a scalar number

Reactance; is essentially inertia against the motion of electrons = express by Xc or XL a complex number

Impedance ;is a comprehensive expression of any and all forms of opposition to electron
                    flow, including both resistance and reactance = express by Z sum of scalar and complex number

 

hope this help to understand

Jagau

Jagau posted this 23 November 2018

To stay in the same idea:


Regarding the nonlinear inductance I noticed in my experimentation that when I use ferromagnetic cores there is a saturation effect that occurs at a certain voltage exceeding the saturation.

Beyond this saturation point we find the non-linearity, it is this section which is difficult to control and to predict it is the one that sudden jumps of voltage and current occurs and this is what we are looking for .

When I did experiments on the generator of don smith the aircore never saturated.

Ferromagnetis material saturates but not air coil.


Jagau

Chris posted this 23 November 2018

My Friends,

Atti, Aloha and Jagau are exactly correct!

Atti, awesome experiments! Thanks for sharing!

Aloha, you're right, the Kapanadze Grenade is a Non-Linear Inductor, as the Current changes so does the Inductance, this effect is very much more pronounced at Resonance. Current reaches its greatest value at the resonance Frequency.

Jagau, thank you, I completely agree! The hysteresis Loop, the B H Curve, up at the Knee, this area is inherently Non Linear because it is moving in and out of Saturation.

 

Normally, the linear sides of the B H Curve are used and the Cores are not normally driven into Saturation, or anywhere near it as a matter of fact. Marked as "Turnaround Point"

 

 

Once Saturated, the Inductance is gone and the Coil presents a simple Resistor, Current can flow through the Coil with no Reactance ( X ). This is how a Saturable Reactor works:

 

I know you know all this already, but for others reading that do not.

   Chris

alohalaoha posted this 23 November 2018

You have made Non linear coil. Question is on which frequency you need to match two traveling waves to get standing wave.

Standing wave is a spatial distribution of nodes and antinodes of current and voltage in the coil

Standing wave calculator

Hey Jagau

Maybe you should try bistabile ferrites with square hysteresis loop ?

Aloha

 

alohalaoha posted this 23 November 2018

Question is why we need to match LC resonance for example from Blue Granade and Standing wave resonance (resonance point where stading wave formation ) is guaranteed ?

Answer in this picture

This is how matching is looking at oscillograph screen.

Upper ray trace - Single pulse excitation. Voltage between ends of matched LC&SW coil. V=20V/div, Timebase = 500nS.

Bottom ray trace - monopolar (unipolar) pulse which run between coil ends, reflect multiple times and fade out.

If you have understood this, you will know why Great Tesla said: "I don't radiate enrgy from my coils (strimers, sparks, corona, etc. etc). I collect energy to huge ammounts and if i need i release that energy in an infinitezimal moment of time.".

ps: This is where has hidden the real power. Keep i mind this is only one pulse excitation.!

Best regards

Aloha

 

 

Chris posted this 23 November 2018

My Friends,

Aloha is entirely correct! We have covered many times the Standing Wave phenomena! Again:

Electromagnetic Wave:

 

 

The Direction of the wave is in the direction of the Blue Arrow. The Wave Length is: λ = v / f - Where v is the speed of light in the medium one is using, and f is the Frequency.

Please forgive my inaccurate depiction, but the following is supposed to show two waves equal, but travelling in opposite directions, the Arrows in the Current Waveform are in the same direction:

 

 

However, the Arrows in the Magnetic Waveform are in opposite Directions! 

Of course, the top and bottom waves in the above Image, when combined, create the wave below: A Standing Wave is the Current depicted in Green, which has double the Amplitude of each wave by itself.

 

Standing Wave:

 

Two Wave Forms, each in opposite Directions, shown by the Blue Arrows. In this case, equal in Amplitude. However we see the Current Waveform, depicted in Green as ( E ), has double the amplitude. This waveform is a Standing Wave, two Current Waveforms traveling in opposite Directions Summing.

The Wavelength for a standing wave is: 0.5 λ

 

My Friends, it is true, the ideal situation, to bring about Non-Linear Coil Conditions, from 90 Degrees on to 180 and from 270 to 360, a Coil, Bucking, Current in opposition, or Partnered Output Coils is one way to achieve these results! 

@Aloha, Current is the Flow of Electrons, and only when a Load is connected can Current flow. When I quoted Ruslan's quote:

2. You need from Tesla only one half wave. Otherwise Tesla will take what she gave, back !!! Therefore, and put the diode from the ground to the very take-off coil (40m) The shark did this at the reception. He removed one part of the sine at the reception itself.

Ref: Ruslan's Flashlight without batteries

 

An answer was given! Ruslan is a smart man, some have said he has faked his devices, I believe none of that! I am very confident he has what he says!

My Friends, you're all completely awesome! I hope now you see why I have said we are light years ahead of the other Forums! We truly are! Please ask questions and we will do the best we can to answer! NO ONE gets trolled here!

   Chris

Jagau posted this 23 November 2018

Hey aloha
excellent discussion
I never try this type of bistable ferrite because it think it is used in frequencies like mcrowave and gigahertz range. Also with the square shape BH also offers a desirable saturation it's just the shape of the curve that changes.
Maybe want to explain more to me what do you mean?

For Tesla yes he used extreme tensions with spark gap that gave him instant energies very great unfortunately I do not work with this kind of tension, maybe one day? Aloha greeting.

Jagau

Chris posted this 24 November 2018

My Friends,

This Thread, without a doubt, is perhaps the most important Thread ever posted to any Internet Forum ever!

The Change of Magnetic Field, which in turn is the Change in Current, the Change in Current Induces an: E.M.F, a Voltage in Conductors: Self-Inductance, and or Mutual-Inductance, all subjected to a Reactance ( X ) to the initial Change in Magnetic Field.

In a Coil, there exists Force between the Wires carrying Current, there is a polarity to this Force:

 

 

 

NOTE: This Force, is not present unless there is a Change in Current and thus a Change in Magnetic Field.

 

 

The Copper tube is Conductive, it does not carry current at all unless the Copper Tube has a Magnetic Interference, this is Electromagnetic Induction!

NOTE: The Copper Tube is not a Source of Current until the Magnetic Field is changing in its proximity, the Currents Changing, or the interference between each other, the Change in Magnetic Flux and the Conductance of the Copper Tube, "Generate" an E.M.F and thus the ability for Current to Flow, the Current is a property of Conductance, not the Magnetic Field!

This is the exact same effect as Self Induction, where the change in Current produces an E.M.F in between the Coiled Conductor, the Wires inside the Coil:

 

 

We have seen the Video, the Lorentz Force, several demonstrations:

 

We have Resistance, Resisting the Change of Magnetic Field, at all stages of Electromagnetic Induction in the form of Reactance ( X ). This is a direct Energy Exchange, Current passing through the Resistance in the Coils, this Energy Transforms into Heat, so Coiled Conductors Heat up as the Current through the Resistance dissipates the Energy.

Newton's Laws of Motion, especially the Third Law, gives us the Secret to Limitless possibilities: For every Action there is an Equal and Opposite Reaction, I have extended this to: and Every Reaction has an Equal and Opposite Counter-Reaction. 

The Secret is Potential, once we have bought the Potential Up, the Reaction can be Counter-Balanced by a Counter-Reaction.

Think of the Conduction of an Insulated Copper Wire, or a Copper Ring, or Tube! There is no Current Flowing in the Copper at all, until it is interfered with. The Change of Magnetic Field is present no matter what happens, it is part of bringing the Potential Up!

This Potential must not be interfered with, its a Prime Mover, the disturbance in the System, to shift the point of Equilibrium. Floyd Sweet gave a figure of genius:

 

 

What goes up, must come down. This we have covered many times. Many different places. One Thread comes to mind: Increasing the Rate of Kinetic Energy.

 

Important: Our Counter Balancing Force I call: Reduced Impedance Effect

 

 

The Forces in the Wires: Forward E.M.F ( Red Arrows ) and the Back E.M.F ( Green Arrows ) are Newton's Third Law in Action: For every Action there is an equal and opposite Reaction!

So we can use The Reduced Impedance Effect to Counter Balance the Back E.M.F ( Green Arrows ), this is introduced as a Third Force!

When Two Coils are positioned in such a way to Buck each other at a specific point in the Cycle, the Coils interfere with each other in exactly the same way the Permanent Magnet "Generating" Currents in the Copper Tube!

 

 

There is a Linear response, the Magnets Distance Traveled / Time, this is the direct result of Lenz Law, but not between our Input and Output Coils, instead this Counter Reaction occurs between two Output Coils, the Forward E.M.F is reinforced, or another way to look at this, using Superposition, is the Magnetic Field Vectors of the Back E.M.F in each Coil are Canceled, they Sum to Zero.

 

This Linear Response is seen as a Saw Tooth Waveform. This is Lenz's Law in Action and is directly seen as Velocity of the Permanent Magnet: Distance Traveled / Time, the Time is slowed dramatically due to the Resistance, the Reactance ( X ), to Change of the Magnetic Field. This is what Tom Bearden called: Asymmetrical Regauging

Ironically, this is information we have been given by those before us:

The magnetic flux from the two secondary windings cancels in the "outer leg circuits," leaving only one-quarter of the total flux generated by the output current to react back upon the primary. This resulted in a current gain in the secondary, relative to the primary. Lenz's law was bypassed, and free-energy resulted. An alternate explanation for the current gain in the UDT is to consider each secondary winding as acting as the primary winding for the other secondary winding when an output current is drawn because the two secondary windings generate geometrically opposing fields.

Now consider the "feedback winding." It is connected in series with the secondary and is wound over the primary winding on the centre leg of the core. When the core is magnetized, an induced voltage will appear across the feedback winding which will subtract from the voltage across the secondary. The purpose of the feedback winding is to cancel the remaining secondary flux passing through the centre leg of the core. It effectively isolates the currents in the primary and the secondary at the cost of a reduced output voltage. The feedback winding generates a magnetic flux equal and opposite to the residual magnetic flux from the secondary when an output current is drawn.

Ref: Paul Raymond Jensen

 

We know Floyd Sweet did have the privilege to study Paul Raymond Jensen's machine. Documented in the Reference link above.

There we have it, we have the ability to change the Inductance at any point we wish, or change the Reactance, the Coil can be Controlled, the Transition of Current through the Coil can be changed by introducing another Equal and Opposite Magnetic Field, an Induced Current, just as the Magnet falling through the Copper Tube "Generated" an E.M.F, we have Coil Conductors doing the same thing.

May still Edit, stay tuned...

   Chris

alohalaoha posted this 24 November 2018

Hey aloha
excellent discussion
I never try this type of bistable ferrite because it think it is used in frequencies like mcrowave and gigahertz range. Also with the square shape BH also offers a desirable saturation it's just the shape of the curve that changes.
Maybe want to explain more to me what do you mean?

For Tesla yes he used extreme tensions with spark gap that gave him instant energies very great unfortunately I do not work with this kind of tension, maybe one day? Aloha greeting.

Jagau

Hey Jagau

By the choice of ferrites, for higher frequency, the lower magnetic permeability should be used, on the low freq, on the contrary, this is due to the ferrite saturation time. Ferrite works fine and gives all the accumulated magnetic field in the region from zero to before saturation points, with the condition of the presence of a demagnetization process. Otherwise, you will get uncontrolled rise of current consumption from the source.

I suspect that Floyd Sweet has rearranged his ferrites to get square hysteresis loop. According to my understanding of ferrite power extraction process, you have a deal with two bistabile spin waves interaction and creation of strong longitudinal shock wave, which also make acoustic resonance of the core. Power of such shockk wave could be so high that in some circumstances could simply smash the core, due to very poor sinteing process.

Regards

Aloha

Jagau posted this 24 November 2018

 

Hey aloha

you quote:

Ferrite works fine and gives all the accumulated magnetic field in the region from zero to before saturation points, with the condition of the presence of a demagnetization process. Otherwise, you will get uncontrolled rise of current consumption from the source.

end of quote

I noticed this effect uncontrolled in the pot core last week, I'm studying this effect now.

Jagau

Vidura posted this 24 November 2018

Hey Aloha and Jagau. I found the this effect of saturation also with the EE ferrite core, at a certain point of powertransfer the core saturates and dont reset itself, o nly when the power is diminished a good deal or disconnected. I guess the effect is much more pronounced when using pulsed or oscillating dc currents. When allowing a small reversed current the core is quickly reset from saturation.

alohalaoha posted this 24 November 2018

Hey Vidura

Yes demagnetization process is crucial. Analyse Floyd Sweet VTA schematic here posted on forum by Chris to understand how he did it with two perpendicular coils.

Also this tool is very needed. Easy build - easy tuning, great results.

Nutz and volts B-H curve tester

http://www.nutsvolts.com/magazine/article/probing_cores

Reg.

Aloha

Chris posted this 24 November 2018

Yes demagnetization process is crucial. Analyse Floyd Sweet VTA schematic here posted on forum by Chris to understand how he did it with two perpendicular coils.

...

Aloha

 

My Friends,

Magnetism is a by product of the Current, the Current, very fast moving Charged Particles! In some Coaxial Cables, the Signal is approximately 78.18% of the Speed of Light. Current is always only just behind the Voltage... We saw, in our Thread: Impulse Pressure Wave, exactly this! Again we see this in the Following Video:

 

Right there, The Fluidic Aether!

NOTE: The Bullet can be thought of as the Fast Moving Charged Particle! The Shock Waves, are the Magnetism, a by product of the Velocity of the Charged Particle.

Also NOTE: A stationary Charged Particle has Zero associated Magnetic Field, the Charged Particle has to have Velocity, be moving!

Magnetism is directly proportional to the Current, in other words, the more the Current, the more the Shock Waves, or Magnetic Field. Concentric Rings are an Artefact of bad Experiment, as when Iron Filings become Magnetised, they in-fact change the underlying Conditions of the Experiment!

 

Ref: youtube   /watch?v=c53hozdkpno

 

After all, what's the Cross Section of a Cone?

 

Current is 90 Degrees to the Magnetic Field, in which direction are Magnetic Particles ( Iron Filings / Compass ) going to align?

The Lorentz Force is the Inertial Turbulence, drive your car behind a Truck and get pulled along, drive past it and feel the push away from it! 

Concentric Rings my goodness, BAD Science!..

There you have it, we have solved one riddle in Science!

 

So, Magnetism is a Wave, we call it an Electromagnetic Wave when it Changes in Time! Again, using the very useful Superposition principle, we only need Cancel the Electromagnetic Wave we don't want!

In other words, the Back E.M.F needs to be canceled by another Equal and Opposite Electromagnetic Wave.

NOTE: Every time a Current is present, or the Potential for the Current to be present, we also have the Potential for Lenz's Law, an Equal and Opposite Current to Oppose, that which created it. The only downfall, is the Time at which these effects take. E.G: 

 

Graham said:

 

 

Here I delay that, so its not a perfect Sine wave, and there is a good reason for that.

 

Look at Grahams Output Current ( Green Waveform ). It takes Time to move through its Cycle. This is the exact same thing as the Permanent Magnet falling through the Copper Tube, Distance Traveled / Time = Velocity. 

 

So, the Potential is bought up on the Coils, the Coils Interact together, Lenz's Law, the Coils Buck and Currents Flow, because we already have an E.M.F, "Generated" in accordance to Faradays law of Electromagnetic induction.

We saw the same things in the Akula Work:

 

 

The Logarithmic change in amplitude, the Curve, is the same exact effect! Its the Magnet Falling Slowly down the Copper Tube!

All are the same! Floyd Sweet, Don Smith, all of them! By using Bucking Fields... Those before us have told us:

An alternate explanation for the current gain in the UDT is to consider each secondary winding as acting as the primary winding for the other secondary winding when an output current is drawn because the two secondary windings generate geometrically opposing fields

 

If the directions of the two signals are such that opposite H-fields cancel and E-fields add, an apparently steady E-field will be created. The energy density of the fields remain as calculated above, but the value of the E-field will double from E / 2 to E.

 

 

 

 

Another answer the Demagnetisation problem, any Core with a Gap, and some materials hold no residual Magnetism. But this is not the solution to the problem. The above is. See Raselli1 videos:

 

Please don't let your selves be distracted though. Like I said, this is not the answer to the current problem!

P.S: I believe Floyd Sweet did use partial Cores, Two Power Coils each having two Cores, split in the middle. It was said he used: Air Cores by Walt Rosenthal. I have no way of proving this however.

   Chris

Vidura posted this 25 November 2018

Hi Chris,

very good the core testing videos from raselli1. I agree that it dont solve the current problem, but could be a proof that the numerous magnetic frames and magnetic current switching devices are possibly operative using the correct core material. 

Regarding the current problem we always face the same issue from lenz law ,action- reaction. Graham states in his presentation that in his device the output current is leading relative to the input, what is generating a positive feedback to the input coil.

->timing

It is stated that the current always lags to the voltage, but if we have an oscillating system time is going in circular path, and we can achieve leading  output current relative to the input and the voltage as well. We have to delay the current flow longer and it passes to the leading position.

I have also read that Floyd Sweet declared his device was basically a time  machine rather than a generator.

regards Vidura

 

 

Chris posted this 25 November 2018

Hey Vidura,

I agree on the Cores!

I have no way to prove this and this is partial speculation. But I believe the Output Current can be "Steered", manipulated.

The Currents assist each other:

 

I believe this "Steering", because in Time, at this stage, the Current is in the direction, becomes additive. The difference of the two Currents, Positive and Negative, in the Output Coils, is Additive. You can see on Graham's trace:

 

The switching on, Yellow Trace ( Input Voltage ), starts the input Current to flow, Blue Trace marked with an arrow, starts a curvature of both the Blue ( Input Current ) and Green ( Output Current ) Traces.

The narrowing of the Traces, converging of the traces, shows effects are still present in the form of Lenz's Law between Graham's Partnered Output Coils.

Regarding Floyd Sweet and Energy / Time, we only ever borrow Energy, it always returns to its source.

   Chris

 

P.S: Ampere-Turn for Ampere-Turn, the Secondary Ampere-Turns > Primary Ampere-Turns, so it only makes sense the Output has a greater Effect. On a Sine Wave, the following Diagram is where we see these effects kick in:

 

The Green line, starting at 270 degrees, ending at 450 degrees, then the Cycle must start again from 450 and again, end, at 630. We do not modify any region from 0 to 90 or 180 to 360, or any region there of, indicating effective part of the Energy "Generation" for both Positive and Negative Slopes of the Sine Wave! However, remembering we have THREE different Currents, so this depends on a perspective and from which Current.

NOTE: One of the Currents in the Partnered Output Coils is Additive to the Input Current, one is not.

Jagau posted this 25 November 2018

Hello everyone
I was away for the last two days and was excited to come back and talk to you.

This subject is very interesting. There is a lot of material to study.


I will take the time to read what has been written in recent days to get back to the subject and appreciate your comments.

Jagau

alohalaoha posted this 26 November 2018

Jagau posted this 26 November 2018

Great video Aloha, it really a new one from this great experimenter.

I did the same with transformer and cap butt in series resonanace ,

but i used a low resistance high power resistor to save my xformer. My osciilosocpe and fluke voltmeter blink and i was a bit afraid of result.

Will make a viseo and show my set up on that soon but with safer method.

Jagau 

Chris posted this 26 November 2018

My Friends,

It surprises me how some people learn things and suddenly think they have discovered a brand-new technology! I have said so many times, many before us have had the knowledge, it's just not yet main stream. We keep reinventing the wheel, the absolute least smartest thing any race can do!  

Tom Bearden was right, he just way over complicated it. Reading the following quote:

That regauging produces two new EM force fields that are equal and opposite, and sum to a vector zero (for translation). This is not exactly a zero force in the truest sense; both force fields are still there and they do continuously act on the system. But there is no NET vector translation force to translation electrons and do work in the circuit, yet there is excess potential energy and there is work being continuously performed on the system. The two force fields do act, and they continually produce stress in the system. The "stress energy" resulting from this activity forms a stress potential added to the system. How one varies that stress potential (magnitude, phase, modulation, etc.) can be very complex and can produce very complex results in materials (particularly in nonlinear material systems, such as a living body).

This stress potential is a change to the energy density of the local vacuum, and the local spacetime. Hence it represents a curvature of the local spacetime (or at least a rotation of the frame of the stressed system, away from the lab frame).

Producing the curvature of spacetime that way is an electrogravitational change. Hence one can make electrogravitational waves, with different magnitudes, frequencies, phasing, modulations, etc.

So one can oscillate the stress potential and all such components, producing a longitudinal (stress) EM wave of sometimes extraordinary characteristics.

For best results, the two opposing waves must not just "mix", but must "modulate" each other and "weld together". For that reason, the effectiveness or noneffectiveness of the coil depends to a great extend on what material is placed inside it as a core material, to perform that "mutual modulation" or "locking".

Depending on the core utilized, the emitted waves can differ. Some can be somewhat hostile or even fairly damaging to humans.

Ref: Principles of the Bifilar coil

 

and 

 

As is well-known, a change of gauge involves only a symmetrical change of both A and Φ EM potential magnitudes (actually, intensities) while the net resultant force field acting on the system remains unchanged because the two new force fields appearing are equal and opposite.

Ref: The Master Principle of EM Overunity

 

A day will come soon, where not one or two successes are bought forward, but hundreds. Its only a matter of these people connecting the dots.

   Chris

Atti posted this 26 November 2018

Hi. Maybe I'm not good at writing this post but I'll fix it if you need it. I do not think I'm telling you anything new I just want to highlight some facts. At least I think so at this time.
Vidura.
A simple transformer with iron and of course a proper arrangement can work with the permanent magnet too. I think it is a must-see essential point to insert the air gap into the transformer circle. I have tried a lot of arrangement without success. Beard's MEG only brought some tension surplus if it was heavily loaded , so the load was influenced by the magnetic force caused by current change.

The total performance is still less.

Another example is the layout of the inkomp delta. It can be clearly seen that if I remove the permanent magnet, the voltage disappears. But this voltage is very small.That is why it needs to be strengthened with a vibrating circuit.That is visible on the video.

Unfortunately, there are fewer removable performance here.

Resonance and two magnetic circles. Recovery and collapse are also evident.

For me, this is a game we can learn a lot from. The facts, the experiment prove even if I do wrong. Everything else is just chattering.
More good work and endurance for everyone!

Chris posted this 26 November 2018

Hey Atti,

Good post, but I have to say I disagree on some points.

Good point on the B-MEG ( Inkomp Delta ), there is no gain in Energy when our Input Opposes Magnetic Flux. However I do think Ivanov had something secret he was not showing.

The MEG does work when one gets the right conditions. A MOV is a Non-Linear Load and this was specified by Tom Bearden, a Non-Linear Load, but he didn't say for both Coils. When implemented correctly, can bring about a Non-Linear Inductance.

I posted some months back that Electromagnetic Induction is not fully understood and stated Electromagnetic Induction is composed of TWO Parts:

  1. The Time Rate of Change of the Magnetic Field ( Current ) "Generates" a Voltage or E.M.F.
  2. Magnetic Field Opposition is the Pump for Current.

 

 

With an infinitely long Copper Tube, the Velocity of the Permanent Magnet would never change. Currents would forever oppose the Permanent Magnets Velocity, the Permanent Magnet would never reach Terminal Velocity.

Endless Current would be Created.

These Currents Created are a by product of Us Placing the Permanent Magnet, not the Cause.

 

 

Three Coils, Three Currents.

People are thinking about this the way Conventional Science has taught them, one needs to force ones mind to open a little further.

   Chris

  • Liked by
  • ISLab
  • Augenblick
Chris posted this 27 November 2018

My Friends,

When I said:

So, the Potential is bought up on the Coils, the Coils Interact together, Lenz's Law, the Coils Buck and Currents Flow, because we already have an E.M.F, "Generated" in accordance to Faradays law of Electromagnetic induction.

 

Potential is Voltage, this costs us very little. Once we have a Potential Difference, the Partnered Output Coils, via Mutual Induction, are Forced to Interact, Isaac Newton's: "What goes up, must come down", kicks in, the Higher the potential the greater the Time taken, the Fall to Equilibrium, the Zero State we started from.

Imagine, the Magnetic Field:

 

 

Then what happens? At the end of the Video, we have a Potential of X, Full Magnetic Field, the Time Rate of Change of the Magnetic Field has created a Voltage on every Conductor in its presence according to Faradays law of Electromagnetic induction. 

The arrangement or Geometry of the System then defines the next step.

The Input Coil is now Off.

Our Voltage or Potential Difference Remains and it must do something, it must return to Equilibrium and as soon as possible. So, by Loading this Potential, we see this:

 

 

The Fall Back to Equilibrium, or Zero State, no Current has Interacted from Primary to Secondary as we saw in the Thread: Some Coils Buck and Some Coils DONT

Remember our Operating Region:

 

 

Green Regions are a go!

Find the optimum Frequency and Duty and the rest is Nature, the Permanent Magnet Falling through the Copper Tube!

This Asymmetrical Arrangement means we have Infinite Current, Infinite Current can be Drawn at no extra cost on the Input. 

   Chris

Vidura posted this 27 November 2018

Hey Atti, your experiments with transformers are very interesting, as you sayd all experiments can lead to more knowledge and discoveries. Therefore posts with practical works and experience are specially valuable. Only I have some difficulties with your language, so I can't understand some details of your setup, maybe you could enable subtitles in YouTube for automatically translation or add a short resume in English, this would be helpful. I have moved a thread about transformer phase shifting for public access again, maybe you can find some information if you are interested. Regards Vidura.

Atti posted this 27 November 2018

Hi Vidura. Unfortunately I do not speak English so I'm compelled to use the google translator.
At youtubon I try to set automatic translation, of course, if you let me. I'm happy to share what I know. If you would describe exactly which part you are interested in, or perhaps better explain it. Atti

Vidura posted this 28 November 2018

Hi Atti, the google translator is fine, not perfect but in most cases it helps to understand basically what is meant. In your transverter video you use two magnetic shunts , how they interact with the core and coils, could you explain or make a drawing how the device (coils) is constructed? What load is connected on the secondary, have you noted an energy gain?

Vidura posted this 28 November 2018

Question is why we need to match LC resonance for example from Blue Granade and Standing wave resonance (resonance point where stading wave formation ) is guaranteed ?

Answer in this picture

This is how matching is looking at oscillograph screen.

Upper ray trace - Single pulse excitation. Voltage between ends of matched LC&SW coil. V=20V/div, Timebase = 500nS.

Bottom ray trace - monopolar (unipolar) pulse which run between coil ends, reflect multiple times and fade out.

If you have understood this, you will know why Great Tesla said: "I don't radiate enrgy from my coils (strimers, sparks, corona, etc. etc). I collect energy to huge ammounts and if i need i release that energy in an infinitezimal moment of time.".

ps: This is where has hidden the real power. Keep i mind this is only one pulse excitation.!

Best regards

Aloha

 

Aloha, when I was rereading this post  I have noted that  in the upper scopeshot  the oscillations after the pulse have a increasing amplitude in the beginning , the energy gain from a positive feedback, is this your experiment? if it is can you give some details from the setup, is it a granadecoil? Regards VIDURA.

alohalaoha posted this 28 November 2018

Hey Vidura.

Everything is so simple you will have laugh. Yes there is 100% energy gain when some conditions have met.

All you need is analog or DSO oscillograph, standard RF signal generator with square wave single pulse or pulses train out, one plastic tube diameter you want , some tenth meters of magnet wire and Vyacheslav Gorchilin's matching calculator.

You need to find correct wire lenght (frequency intersection point) for exact matching both stuffs, LC resonane of the coil (inductance plus self capacitance) and standing wave resonance (correct phase of incident and reflected wave which would create stabile standing wave in your lambda/4 coil. Whole process is autosync. Just fire an impulse and watch.

WOULD BE EXTREMELY INTERESTING THAT SOMEONE MAKE THIS WITH MATCHED PARTNERED COILS. Of course every single CW & CCW coil should be tuned independently and then both connected in partnered configuration or even looped to form a short circuit and than watch what single square wave pulse will do in such configuration.

Regards

Aloha

 

Atti posted this 28 November 2018

Hello Vidura and everyone.

 

The presented transformer iron is a simple MOT of coils of the original primary coils. It is true that another similar one has been used. The inductance data therefore differs slightly as can be seen in the video. Hipersil iron is good but it needs to be further energized. I believe that the core is saturated. If it is no longer possible to close the main line in the main column, it is forced to close through the short circuit in the jar. This results in two magnetic paths.

 

If we roughly compute the apparent performance we can see the multiple deviation. But unfortunately this is bad. If that's what I'm suffering, the whole resonance crashes and is like nothing had happened. Eliminates higher secondary current and voltage. I tried to load a timer circuit, but it was also unsuccessful. A similar composition can be seen in this old video. Right here I tried the inkomp delta magnetic transformer. Here I tried to combine the two resonances.

5:25 minutes it can be seen that if I only connect the bulb as a pulse, the voltage of the capacitor will rise to 10-120V because of the load change
6:45 is visible. With continuous load, only 13 volts.

For this reason, I now think that there are two configurations in the layout where there are two transformers, but taking into account the above. But I may be on the wrong road. Good job for everyone.

Chris posted this 29 November 2018

My Friends,

@Atti - Nice Work! Thanks for sharing.

As Atti has shown, the Inductance changes with a Non-Linear Curve when the Coil with a Core moves in and out of Saturation. Jagau also stated the same thing.

The Knee of the B H Curve, where we see this region of Non-Linear Inductance, is marked in Red:

 

 

Please Note: This is not the only way to Invoke a Non-Linear Inductance!

Inductance Changes with the Magnetic Field, I did a bit of a study on this here: Saturation

Keep in mind back when I did this set of experiments, my terminology was not the best, so please be a bit forgiving of my writings.

No more Magnetic Flux can traverse a Saturated Path. Saturated, like a Sponge, means no more Magnetic Flux can be contained in the Core, in the same direction, as no more water can be contained in the Sponge.

However, I would like to remind you, that there is likely more to this than just Inductance.

   Chris

Chris posted this 29 November 2018

My Friends,

I recommend we revisit the Concepts I have shown on Partnered Output Coils. I stated some time back:

Hey Brad, you already know how it works, I don't need to do any homework or thinking for you.

Like I said, three Coils, one input, two output, go for best result...

Persistence and common-sense as you already know is the key to getting a result.

If you were to break down your RT we see the same thing, three Coils, you had a Velocity component, on the Rotor, that is not directly evident in the Transformers I build, but its still there, Graham Gunderson shows it. Which I will admit I did not notice until recently.

Ref: Partnered Output Coils - Free Energy

 

Brad visits us here at aboveunity.com, from Perth, Gelorup, Western Australia, for information even as recent as a few days ago.

Like The Mr Preva Experiment, one needs to get the Currents in the Output Coils Opposing! Then we see a purely Non-Linear Inductance.

 

 

Remember all the Greats before us, remember, you must catch the Wave, the Sawtooth Wave down, this is the Magnet Falling down the Copper Tube. The Sawtooth Waveform, once Caught, this is where you see an excess of Electrical Energy! Covered in detail in: Asymmetrical Regauging

This is a Requirement!

So, the procedure:

  1. Input Coil ( Green Coil ) brings up the Potential, then is switched Off.
  2. One Output Coil then Conducts Current ( Gold Coils ).
  3. The Second Output Coil then also conducts Current, a split second after the first, Equal and Opposite, to the First Output Coil ( Gold Coils ). Exactly the same as the Magnet and Copper Tube Experiment!

 

Some simple circuitry can make this happen, or some very simple Geometrical additions.

I promise you my friends, when this is done and done right, this will produce COP > 1 Energy Machine!

An AboveUnity.com Machine!

  • Absolutely no Magic!
  • Absolutely nothing special!
  • Absolutely nothing you cant buy from a shelf!
  • Simple and clean.

This is super simple visually, super cheap, but not so easy to get a result. Some Fiddling is required!

   Chris

 

Vidura posted this 30 November 2018

Chris, 

there is something that have not been mentioned in POC discussions(i think). In the image there is a divided core with two points faceing each other, some explication for this? Concentrating the magnetic field in a very small point?

  • Liked by
  • Chris
  • Augenblick
Chris posted this 30 November 2018

Hi Vidura,

The Red Arrows are the Magnetic Field Vectors. Each Equal and Opposite.

So the Partnered Output Coils must Buck, if they are not Bucking, then they are not working properly! This is the biggest problem so many have had!

We saw exactly this in The Mr Preva Experiment and the reason I have tried so hard to push that experiment! Getting people familiar with that Concept.

The Central Point does hold value Vidura. It is a region of maximum Coupling Coefficient between the Coils. I have said many times, more so in the past, the requirement is Loose Coupling, or be Loosely Coupled, some use the term Flux Leakage. I have had no luck with Unity Coupling at all over the years, although, I think it can be done.

Unity Coupling
An Ideal coupling between two inductors, so that entire magnetic field of one inductor passes to the second inductor.

I always think of this as, Secondary wound full length and on top of the Primary.

   Chris

 

P.S: These last few posts and the latest Threads are perhaps the most important ever - SO PLEASE MAKE SURE YOU HAVE NOT MISSED POSTS...

  • Liked by
  • Zanzal
  • Augenblick
Chris posted this 01 December 2018

My Friends,

In specific relation to the above few posts, I wish to point out Geometry.

If we turn the following image on its end:

 

 

Like so:

 

 

And if we imagine the Fields in Time, we do in-fact get a similar visualisation to the following:

 

 

 

Evidence for the most efficient Moving Masses we have ever studied:

 

 

It may be that The Flow of Energy is part of the geometrical Energy itself. We have seen some of this before. I believe this is about Reducing the over all Impedance.

   Chris

  • Liked by
  • Augenblick
  • ISLab
scalarpotential posted this 11 April 2022

Hi, you say: Inductance ( L ) is the Rate at which Amperes can flow through the Coil in Time, this is defined as: L = di / dt

This seems to me incorrect. inductance L is the flux capacity, the amount of generated and 'stored' flux per admitted ampere, just like C is the amount of stored coulomb per created voltage. L=N.dphi/di
the next one was correct: L=emf/di/dt from emf = L.di/dt.

  • Liked by
  • Augenblick
Chris posted this 11 April 2022

Hi ScalarPotential,

In the first post I give you supporting links, you can read more there to learn about inductance.

I believe, you will come to the conclusion, that we are talking the same things. Ampere Turns NI defines Flux Φ for the most part, and Amperes Law will assist you in proving this.

Best Wishes,

   Chris

  • Liked by
  • Augenblick
We're Light Years Ahead!
Our Above Unity Machines:

Asymmetrical EMI

Wistiti's Bucking Joule Thief
Non-Inductive Coil Experiment
CD's Non-Inductive Coil Rep
Baerndorfer's Experiment
Captainloz's A-R-E
Aetherholic's COP>4.0

Resonant EMI

Yo's Ferro Resonance
Jagau's Non-linear Resonance
Ferrite at work
Recomended Protocol:
Measurement
Switching System
Measurement Block
Current Observation
Current Sensing Resolution
Members Online:

No one online at the moment

What is a Scalar:

In physics, scalars are physical quantities that are unaffected by changes to a vector space basis. Scalars are often accompanied by units of measurement, as in "10 cm". Examples of scalar quantities are mass, distance, charge, volume, time, speed, and the magnitude of physical vectors in general.

You need to forget the Non-Sense that some spout with out knowing the actual Definition of the word Scalar! Some people talk absolute Bull Sh*t!

The pressure P in the formula P = pgh, pgh is a scalar that tells you the amount of this squashing force per unit area in a fluid.

A Scalar, having both direction and magnitude, can be anything! The Magnetic Field, a Charge moving, yet some Numb Nuts think it means Magic Science!

Start Here:
Help with using the Forum.
Message from God:

Hello my children. This is Yahweh, the one true Lord. You have found creation's secret. Now share it peacefully with the world.

Ref: Message from God written inside the Human Genome

God be in my head, and in my thinking.

God be in my eyes, and in my looking.

God be in my mouth, and in my speaking.

Oh, God be in my heart, and in my understanding.

Your Support:

More than anything else, your contributions to this forum are most important! We are trying to actively get all visitors involved, but we do only have a few main contributors, which are very much appreciated! If you would like to see more pages with more detailed experiments and answers, perhaps a contribution of another type maybe possible:

PayPal De-Platformed me!

They REFUSE to tell me why!

We now use Wise!

Donate
Use E-Mail: Chris at aboveunity.com

The content I am sharing is not only unique, but is changing the world as we know it! Please Support Us!

Thank You So Much!

Browse by Category:
Weeks High Earners:
The great Nikola Tesla:

Ere many generations pass, our machinery will be driven by a power obtainable at any point of the universe. This idea is not novel. Men have been led to it long ago by instinct or reason. It has been expressed in many ways, and in many places, in the history of old and new. We find it in the delightful myth of Antheus, who drives power from the earth; we find it among the subtle speculations of one of your splendid mathematicians, and in many hints and statements of thinkers of the present time. Throughout space there is energy. Is this energy static or kinetic? If static, our hopes are in vain; if kinetic - and this we know it is for certain - then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.

Experiments With Alternate Currents Of High Potential And High Frequency (February 1892).

Close