• Understanding and Exploiting Physical Phenomena

Understanding and Exploiting Physical Phenomena

  • 1.7K Views
  • Last Post 05 January 2019
Prometheus posted this 25 September 2018

Sorry if this is in the wrong topic, feel free to move it if need be.

Ok, let's discuss magnets. Most of this everyone will know, but I'll start at the beginning so newbies can come up to speed.

Magnetism is a purely quantum mechanical phenomenon. Classical physics cannot account for diamagnetism (and hence cannot describe the underlying mechanics of the existence of invariant-mass matter), as Niels Henrik David Bohr showed in his doctoral dissertation in 1911, which is known today as the Bohr-van Leeuwen theorem.

 

THE TINIEST MAGNETS IN THE UNIVERSE
----------
First, we'll discuss the tiniest (electro)magnet in the universe... the electron. A bound electron being a point charge undergoing (angular) acceleration (the two requirements for the emission of virtual photons, known as Larmor radiation... which manifests as a magnetic field), bound electrons produce a magnetic field having a magnetic moment along the axis of rotation.

The spin of electrons (free or bound) also produces a magnetic moment along the spin axis (and in fact, the primary contribution to the bulk magnetic field of a permanent magnet is due to electron spin), so even free electrons emit Larmor radiation, but we'll stick with bound electrons because they reveal some very important details about how the universe works.

Now, quite obviously, the emission of virtual photons means that a bound electron is constantly emitting energy (photons being force-carrying bosons which mediate the EM fundamental force). How does the bound electron avoid 'spiraling in' to the oppositely-charged proton(s) in the nucleus of the atom to which the electron is bound? It obtains energy from the non-zero expectation value of the quantum vacuum.

In particle physics, any dipole (as is a magnet) is a broken symmetry in virtual energy exchange between the quantum vacuum and the charge(s) forming the dipole. Thus quantum physics classifies magnetism as a pseudovector to ensure that electromagnetism does not violate parity symmetry under reflection . I'll discuss this further below.

It should be noted that some physicists consider a bound electron in its ground-state orbit to be in a 'net zero emission' state... but that's tricky-wording the issue. The word 'net' implies that emission is perfectly balanced by absorption of energy, which is what Boyer et. al. showed all the way back in 1975, and revisited the topic in 2015:
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.11.790
https://arxiv.org/pdf/1511.02083.pdf

Cole and Zou also addressed the topic:
http://www.bu.edu/simulation/publications/dcole/PDF/DCColePhysicsLettA.pdf

As did Haisch and Ibison:
https://arxiv.org/ftp/quant-ph/papers/0106/0106097.pdf

As did Hal Puthoff:
https://arxiv.org/ftp/arxiv/papers/1204/1204.1952.pdf

As did NASA:
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20150006842.pdf
"A thing to note is that the integral of the perturbation of the quantum vacuum around the nucleus for a given atomic number Z and quantum number n is exactly equal to the energy level of the electron in that state. The energy level of the electron is a function of its potential energy and kinetic energy. Does this mean that the energy of the quantum vacuum integral needs to be added to the treatment of the captured electron as another potential function, or is the energy of the quantum vacuum somehow responsible for establishing the energy level of the "orbiting" electron? The only view to take that adheres to the observations would be the latter perspective, as the former perspective would make predictions that do not agree with observation."

 

Order By: Standard | Newest | Votes
Prometheus posted this 25 September 2018

IT'S A HARD-KNOCK LIFE (for atoms)
----------
Every atom is a brutal environment... the proton(s) in the nucleus have an outward pressure of ~145,037,737,700,000,000,000,000,000,000,000 psi (about 10 times greater than the inward pressure in the center of a neutron star), held together by the strong force.
https://www.nature.com/articles/s41586-018-0060-z

The electron(s) are whipping around the nucleus at high speed (~2,190 km/s), orbiting ~6,500,000,000,000,000 times per second. In the tiny distance (~0.0000000001 m) between the bound electron(s) and nucleal proton(s) there is an extremely strong electrostatic force (~1,000,000,000,000 V/m), high enough to polarize the vacuum (which is how virtual photons (Larmor radiation) are manifested from the quantum vacuum by the bound electron to begin with).

A bound electron must have an integer number of de Broglie waves in its spherical orbit (the underlying basis for quantization and hence Quantum Mechanics), or it sets up a destructive-interference orbit, causing the electron radius to decrease until an integer number of de Broglie waves exist in the orbit. The amount of energy added to a bound electron's orbit must be sufficient to add at least 1 de Broglie wavelength to the orbit or the energy is reflected rather than absorbed:

The sinusoidal (2D) / spiral (3D)


quantum vacuum wavemodes of the correct frequency can constructively-interfere with the electron's de Broglie waves to impart momentum to the electron, sustaining it in its orbit about the nucleus. It is believed that this occurs via a loop divergence which contributes energy to the electron via absorption and emission of many virtual photons manifested from the quantum vacuum as a result of the vacuum polarization in the high field strength environment of the nucleus-electron interstitial space.

{ASIDE}
----------
In the images above, you'll note the peak amplitude of the sinusoid is analogous to the radius of the circle, the peak-to-peak amplitude is analogous to the diameter of the circle, and the frequency of the sinusoid is analogous to the rotational rate of the circle. You'll further note the circumference of the circle is equal to 2 * pi radians, and the wavelength (wave period... the inverse of frequency) of a sinusoid is equal to 2 * pi radians, so the wavelength of the sinusoid is analogous to the circumference of the circle. Why is this? Well, it's because a sinusoid is a circle, spread out over space and time! It's a spiral. What we see on an oscilloscope is a sinusoid, but that's just a shadow of a deeper reality (hint: try stretching out a Slinky in bright sunlight... the shadow will be a sinusoid).

You'll find the Real (labeled 'Re' in the first image above) and Imaginary (labeled 'Im' in the first image above) components of a waveform's sinusoidal (2D) / spiral (3D) form also correspond to the magnetic and electric components of that waveform. So magnetism is a geometrical transform of a moving electric field (and vice versa), a change of reference frame.
----------
{/ASIDE}

Thus the non-zero expectation value of the quantum vacuum underpins the stability of all invariant-mass matter. By corollary, this also means ALL elements exhibit magnetism (usually diamagnetism, although certain elements have electron valency configurations which override the inherent diamagnetism with paramagnetism, ferromagnetism, ferrimagnetism or antiferromagnetism).

You'll note that only certain frequencies of quantum vacuum wavemodes can contribute energy to the bound electron, dependent upon the electron's spin frequency, de Broglie wavelength and orbital angular frequency. Thus as an electron's orbital radius increases, the quantum vacuum wavemodes which can constructively-interfere to contribute energy to the electron's orbit must be longer in wavelength (orbital angular frequency decreases) and therefore less energetic... this prevents the quantum vacuum from adding so much energy to the bound electron that it self-ionizes. On the other hand, when electron orbital radius decreases, its orbital angular frequency increases, so the quantum vacuum wavemodes which can constructively-interfere to contribute energy to the electron's orbit are shorter-wavelength (more energetic), preventing the electron from 'spiraling in' to the oppositely-charged proton(s) in the nucleus despite the extremely strong electrostatic forces and the electron's emission of Larmor radiation.

The above is why Casimir cavities can block specific frequencies to generate an artificial Lamb shift and thus force the bound electrons of a noble gas to emit photons, as Haisch and Moddel (and Dmitriyeva and Moddel) showed:

http://ecee.colorado.edu/~moddel/QEL/Papers/US7379286.pdf
http://ecee.colorado.edu/~moddel/QEL/Papers/DmitriyevaModdel12.pdf

The above clashes with conventional theory (as taught in colleges worldwide), which states that as an electron gets closer to the nucleus its kinetic energy goes upward toward infinity and its potential energy goes downward toward negative infinity. Of course, nothing massive can exceed c (the speed of light in a vacuum), so an electron's kinetic energy is limited by its small mass and by the fact that its speed cannot exceed c, so the conventional explanation doesn't make a lot of sense. How does conventional physics get around the problem of Larmor radiation emission by the bound electron undergoing angular acceleration? They claim an electron in its ground state orbit has no orbital angular momentum, and therefore cannot emit Larmor radiation! As if the ground state orbital radius is somehow different than any other orbital radius in any manner other than its radius.

To be fair, there is a "magic moment" kinetic energy of a bound electron, in which the magnetic moment is parallel to the direction of orbit and therefore no Larmor radiation can be emitted (rather, it is emitted, but is immediately reabsorbed by the electron since that energy is directly inline with the electron's orbit), but the electron's "magic moment" kinetic energy is ~14.5 MeV, whereas the electron's ground state kinetic energy is on the order of only eV (for instance, the hydrogen atom's ground-state electron kinetic energy is 13.6 eV). Even the rest mass of an electron is only 0.510998946113 MeV, so unless the electron's in an unusually energetic environment (such as a particle collider), it's not going to reach ~14.5 MeV of kinetic energy.

The problem with the above contention by conventional theory is that it also leads to the conclusion that there is no mechanism in conventional theory by which an electron could be induced to go lower than its ground state orbital radius (the two infinities cancel)... except we know it can, and we know why it can. Haisch and Moddel proved it empirically by artificially lowering quantum vacuum expectation value in a plethora of Casimir cavities, which caused the electrons of a noble gas to lower their orbital radius below their usual ground state radius and thereby emit photons. In fact, they've even got a patent (U.S. Patent 7379286, linked above) on the process.

Prometheus posted this 25 September 2018

HOW MAGNETS ARE MADE
----------
Next we'll discuss how a permanent magnet is made...

Typically, a modern magnet is made of sintered material, a ferromagnetic powder. Before the magnetic powder is pressed and sintered, a strong external magnetic field is applied, which aligns the particles in the magnetic powder along their easy axes (the anisotropic axis of the crystallographic lattice which minimizes the magnet's internal energy via spin-orbit coupling (which can be quite large for crystallographic lattices with uniaxial symmetry) with the crystal field (of Crystal Field Theory (CFT)), and thus the easy axis is the preferred magnetic moment direction of each particle). While still in the strong magnetic field, the powder is pressed and sintered above its Curie temperature. As the external magnetic field strength is increased, the magnetic domains align in the direction of the external field (which also happens to coincide with the magnetic material's easy axis). This alignment is known as coherent rotation. If two domains come into perfect magnetic moment alignment, it is energetically favorable for the domains to eliminate the domain wall between them, so the domains join into one larger domain.

If the external magnetic field is increased further, the magnetic material will become magnetically saturated, all the domains will align and therefore join (if there are no defects or stresses in the crystalline lattice of the magnetic material), creating one single domain. The magnet is then allowed to cool while still in the external field.

The alignment of the easy axes and the external field is done because coherent rotation is reversible... once the external field is removed, the magnetic moments can reorient to the easy axis direction of each particle of ferromagnetic powder... but if all the easy axis directions are in the same direction, and that direction is the same as the direction of the external field's magnetic moment, then no decoherence will take place, making for a stronger magnet.

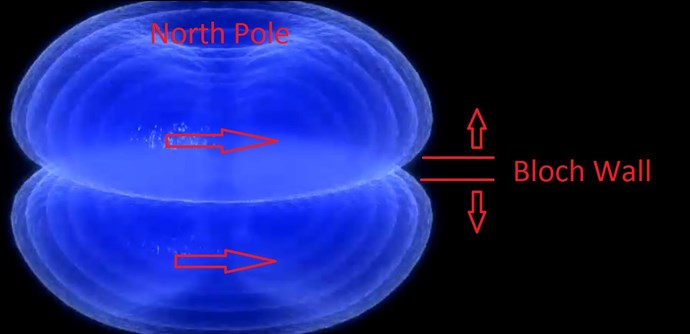
"But if a magnet is made into a single domain by magnetically saturating it during the magnetization process, why does a Bloch Wall exist at the centerline of the magnet?", you may be asking. That's a very good question, one which isn't addressed in many places online, and is glossed over in most other places.

A Bloch Wall is a region where the predominant magnetic moment direction changes between two domains, therefore the magnetic domains within the Bloch region gradually cant their magnetic moment as a means of minimizing the exchange energy between those domains. A Bloch Wall is typically 100 to 150 atoms thick, rather than being only 2 atoms thick, because the exchange energy between the domains is lower when distributed over many electron spins.

The domain wall thickness is determined by the competing influences of the magnet's magnetoelastic crystallographic anisotropy which strives for: 1} magnetic moment alignment along the easy axis and 2} thinner or nonexistent walls (because magnetic moments pointed away from the easy axis, as would occur in a Bloch Wall, are higher energy due to magnetostriction); and the exchange interaction which strives for: 1} parallel magnetic moments and 2} thicker walls between non-aligned domains (because large angles between neighboring non-aligned spins, as would occur in a thin Bloch Wall, is energetically unfavorable for the exchange interaction).

So the question remains... if the easy axis is aligned with the predominant magnetic moment and the magnetic material is magnetically saturated in an external field during magnetization such that the magnetic crystallographic anisotropy requirement is satisfied to the point that the magnet is one giant domain, and therefore all magnetic moments are parallel and thus the exchange interaction requirement is satisfied, why then do we see a Bloch Wall at the centerline of the magnet?

Obviously there's a change in the predominant magnetic moment direction at the magnet's centerline, despite the fact that the magnet was saturated to the point of becoming a single domain. The very existence of the Bloch Wall at the centerline of the magnet proves this!

Why does this happen?

To explain this, we have to dive into electronic band structure and the Stoner Model of Ferromagnetism. I arrived at the same conclusions as the Stoner Model without benefit of knowing about it, but since it mirrors what I've learned, we'll stick with its precepts.

In solid-state physics, the electronic band structure of a solid describes the range of energies (energy bands) that an electron within the solid may have and ranges of energy (band gaps) that it may not have. Electron bands can spontaneously split into up and down spins. This happens if the relative gain in exchange interaction (the interaction of electrons via the Pauli exclusion principle) is larger than the loss in electron kinetic energy.

The Stoner Model and Fermi–Dirac Statistics explain electron spin-spin interaction within a permanent magnet, and why the magnet develops a Bloch Wall. Locally, the valence electrons align the non-conductance electrons of neighboring atoms. The non-conductance electrons of one atome have, for instance, spin-up, which forces the conductance (valence) electrons into spin-down, which forces neighboring non-conductance electrons into spin-up, thereby aligning the electron spin directions and thus the magnetic moments. This is how magnetic domains grow.

Hund's Rules (specifically Rule 1) state that the first few electrons in a partially-filled shell tend to have the same spin, thereby increasing the total dipole moment, and that therefore the spin states of those electrons are affected together... so if one flips, they all flip. The energy gain that motivates Hund’s Rule #1 is that the Pauli exclusion principle keeps electrons with the same spin further apart on average, thereby lowering the Coulomb repulsion (atomic exchange energy) between them.

The Pauli exclusion principle states that two electrons with the same spin cannot occupy the same space at the same time. Therefore when the orbitals of the valence electrons from adjacent atoms overlap, the distributions of their electric charge in space are farther apart when the electrons have parallel spins than when they have opposite spins. Thus they have the same spin direction and spread out more to minimize their atomic exchange energy.

Once the ferromagnetic material has its domains aligned in a magnetizer (during which, the energy added by the external magnetic field allows the magnetoelastic crystallographic anisotropy to "win out" temporarily, creating a single large domain), the exchange interaction splits the energy of states with different spins (exchange splitting), and states near the Fermi level (a hypothetical electrochemical potential of an electron (which we simplify to voltage), such that at thermodynamic equilibrium this energy level would have a 50% probability of being occupied at any given time) are spin-polarized (band formation and hybridization) simply because the magnetic material has insufficient magnetic hardness to prevent the electrons flipping their spin direction (and thus their magnetic moments).

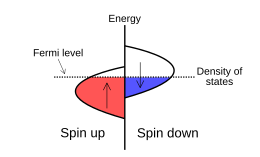
So while the magnetoelastic crystallographic anisotropy prevails during magnetization (for materials which have their easy axes aligned prior to sintering), the exchange interaction will not be denied its due, and will flip some electron spins to minimize the magnet's internal energy.

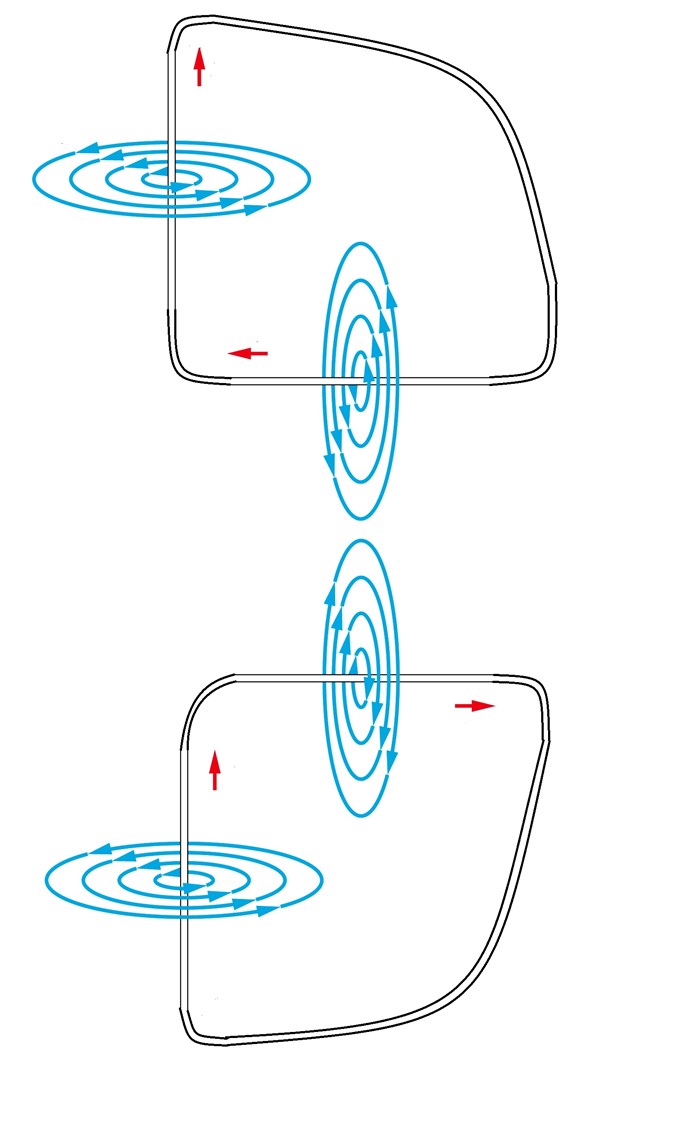
The whole process of domain flipping starts because of the H (stray or demagnetizing) field... although during magnetization the magnet may be a single domain, the stray field sets up surface currents which create stray magnetization which begins subdividing the surface into magnetic domains, which propagate in three dimensions through the magnet, meeting at the midline of the magnet, where the Bloch Wall is formed.

Thus, approximately half the electron spins (and thus approximately half the domains) flip 180 degrees. These domains are interspersed throughout the magnet. It is hypothesized that the domains of the two predominant magnetic moment directions 'twist' through the body of the magnet (forming vortices and antivortices), thereby avoiding opposing domains while allowing virtual photon flux a route through the magnet. ETH Zurich have used X-ray vector nanotomography (circular polarized hard x-rays) and showed that there is preferential absorption of certain light polarizations, which manifests as a change in the diffraction pattern of the light, which allowed them to view the magnetic field:
https://www.nature.com/articles/nature23006
https://phys.org/news/2017-07-first-time-d-imaging-internal-magnetic.html


"We imaged the structure of the magnetization within a soft magnetic pillar of diameter 5 micrometers with a spatial resolution of 100 nanometers and, within the bulk, observed a complex magnetic configuration that consists of vortices and antivortices that form cross-tie walls and vortex walls along intersecting planes."

The cumulative effects of the two resulting predominant magnetic moment directions meet and cancel at the midline of the magnet, which is what we call the Bloch Wall (although the walls between all the domains in the magnet are typically Bloch Walls, as well, unless the material is so thin that the magnetic moments cannot flip out of plane, whereupon they form Neel walls, with the magnetic moments rotated in-plane). The domains at the magnet's midline (Bloch Wall) are canted (angularly displaced) in different directions (typically 90 or 180 degrees out of plane over 100 to 150 atom widths) to minimize the energy of the magnet, just as the domains in the rest of the magnet are oppositely-aligned for the same reason. The difference is that there is nothing at the Bloch Wall region to force the domains into diametrically-opposed magnetic moments (there is no force exterior to the magnet acting upon those domains). For this reason, the Bloch Wall of a magnet can be considered to be 'unmagnetized'. This also implies that the Bloch Wall at the midline of a magnet is a surface phenomenon, likely not extending more than a few hundred atoms in depth.

 

Prometheus posted this 25 September 2018

SOLILOQUIZING AND THEORIZING:
----------
So while most people believe the process of magnetization of ferromagnetic material gives us a 'dipolar' magnet, with a North pole and a South pole, the naming convention was made long before quantum mechanics came into being, and is a bit misleading... because while a magnet does indeed have a North pole and a South pole, it actually has 4 interfaces with the quantum vacuum, 2 on each pole face!

A magnet isn't really 'dipolar'... it's 'quadra-interfacial'... 4 interfaces with the quantum vacuum (two on each pole face). To be completely correct, we must state that a magnet is pseudovectoral, because the two poles are a result of an improper isometry (a three-dimensional reflection) as mentioned above. This is a result of the EM interaction's conservation of parity. The magnet's electric field (from the orbiting electrons) is a vector, but the magnetic field is a pseudovector. However, Maxwell's equations are parity invariant because the curl of a pseudovector is a vector (and vice versa), and B = curl(A).

Thus, in every magnet there are actually four interfaces with the quantum vacuum, two on each pole face. The North pole and South pole are identical except for the direction of the curl of the magnetic vortex entering or leaving the magnet's pole faces.

Because of the above, interspersed throughout a typical magnet there are actually two magnets and thus two virtual photon flows:
1) From the center of Pole Face 1 (let's say it's the North pole), to the perimeter of Pole Face 2 (let's say it's the South pole).

2) From the center of Pole Face 2, to the perimeter of Pole Face 1

{NOTE: This is the virtual photon flow internal to the magnet.}.

This is why you can cut a magnet, and each cut piece will still have a North and South pole. After being cut, each cut piece will rearrange their domains (at the magnetic diffusion rate for that magnetic material) such that a new Bloch Wall will form at the midline of each cut piece, by the same process by which the Bloch Wall formed in the uncut magnet.

So virtual photons are pulled out of the quantum vacuum and into the center of the North pole face (a low field radiation pressure region), the virtual photons follow the domains which are aligned in the same direction, and are emitted at the perimeter of the South pole face (a high field radiation pressure region), whereupon they are subsumed back into the quantum vacuum.

Simultaneously, virtual photons are pulled out of the quantum vacuum and into the center of the South pole face (a low field radiation pressure region), the virtual photons follow the domains which are aligned in the same direction, and are emitted at the perimeter of the North pole face (a high field radiation pressure region), whereupon they are subsumed back into the quantum vacuum.

What determines whether the virtual photons go North pole to South pole, or South pole to North pole? Their helicity (the intrinsic angular momentum as compared to the direction of motion). Helicity can be either +1 or -1. Intrinsic angular momentum cannot be portrayed in a linear reference frame except by projecting the rotational magnitude along the line of the reference frame (ie: casting a shadow of the angular momentum, which is a transform and gives us a sinusoid).

The helicity of the virtual photons must align with the spin direction of the bound electrons, and the only difference between the photons flowing out of either pole face is their helicity.

You'll note we must force a ferromagnet to become a ferromagnet (even lodestone, magnetite minerals in basaltic rock, were magnetised by being struck by lightning). It doesn't happen spontaneously because the internal energy of a magnet is higher than the ground energy state for that magnetic material. In so creating a magnet, what we're doing is setting up a time imparity in the magnet (because the magnetism we use in creating the magnet stresses the QVZPE field and thus affects space-time, as discussed below), which is locked into place because of the intrinsic crystalline composition of the magnet... so you might say a magnet is ditemporal, allowing the magnet to experience a simultaneous (from our perspective) time-shifted (from the magnet's perspective) energy over-abundance and energy deficit, which causes the magnet to throw off / take in virtual photons to / from the QVZPE field.

In essence, a ferromagnet is a folded strange attractor. To put it to a very simplified analogy, it's two cross-flowing whirlpools of virtual energy from the quantum vacuum, put into motion by the temporal effects of the induced coherent magnetic field which is locked into place by the magnetic hardness of the magnetic material.

Prometheus posted this 25 September 2018

A MAGNET'S EFFECT UPON SPACE AND TIME
----------
Because a magnet has two interfaces with the quantum vacuum (inflowing, outflowing) on each pole face, there is a lower field radiation pressure region at the center of each pole face, and a higher field radiation pressure region around the perimeter of each pole face.

Given that the quantum vacuum is, quite literally, the fabric of space-time, the differing quantum vacuum field radiation pressures have effects upon space-time. You'll note that this doesn't mean that the quantum vacuum is space-time, however. The quantum vacuum can affect space-time, but it is not space-time.

The correlative effects of Zero Point Radiation (ZPR) upon space, time and gravity:
ZPR increases: GRAVITY decreases, SPACE-TIME CURVATURE decreases, SPACE contracts, TIME evolves faster.
ZPR decreases: GRAVITY increases, SPACE-TIME CURVATURE increases, SPACE expands, TIME evolves slower.

The Inflowing interface at the center of each pole face of a magnet (where virtual photons enter the magnet) slows time down and expands space by reducing quantum vacuum field radiation pressure.

The Outflowing interface around the perimeter of each pole face of a magnet (where virtual photons leave the magnet) speeds time up and contracts space by increasing quantum vacuum field radiation pressure.

Howard Johnson was the first to explicate the vortexual nature of magnets (and the interspersal of opposing domains throughout the bulk of the magnet), although he got the sign wrong and his measurements showed two spatially separate vortexes on each pole face... in order for magnets to comport with Quantum Mechanics and General Relativity, they must stress the quantum vacuum in the manner described above. I believe Johnson's findings were skewed by the fact that he was using a cubic magnet, which introduces macroscopic shape anisotropies. A cylindrical magnet, magnetized through its length, would have proven the concept described above, that of two cross-flowing vortexes through the length of the magnet.

On each pole face, because the two predominant magnetic moment directions are interspersed, the effects tend to cancel out (which, by the way, is the reason we must introduce the relativistic effects of motion in our electrical generators). But you will note that an iron ball placed on a large magnet will tend to roll to the perimeter of either pole face, because iron (being a ferromagnetic material) seeks the highest field radiation pressure, just as iron filings tend to align along the highest magnetostatic flux lines. So the effects don't completely cancel out.

A gravitational field represents a curvature (expansion) of space-time. Anything that carries energy (including invariant-mass matter, which is merely another form of energy) or momentum (ie: a stress-energy tensor) causes a curvature of space-time. In fact, this is how magnetic attraction and repulsion works... by increasing quantum vacuum energy density above ambient, or decreasing it below ambient. Magnetism isn't, however, gravity... gravity due to invariant-mass is unidirectional toward that mass (ie: mass can only expand space-time by rejecting and shielding quantum vacuum wavemodes, thereby lowering quantum vacuum field radiation pressure), whereas magnetism can expand or contract space-time, causing attraction or repulsion. Two different causes via the same mechanism upon the same medium.

Magnets opposite-pole to opposite-pole (N to S) reduce quantum vacuum field radiation pressure, causing an expansion of space-time and thus an energy "well" (lower energy density due to expanded space) (although not considered a "gravity well") which objects attempt to 'fall' into, which we perceive as attraction. Magnets like-pole to like-pole (N to N, or S to S) increase quantum vacuum field radiation pressure, causing a contraction of space-time and thus an energy "hill" (higher energy density due to contracted space) which objects attempt to slide down, which we perceive as repulsion.

 

Prometheus posted this 25 September 2018

THE RESEARCH, THE EMPIRICAL
----------
How do we know these effects take place, what corroborates the above explicative exposition? Well, we have research on the topic, and some empirical examples.

For instance, invariant mass matter rejects quantum vacuum wavemodes which don't correspond to the electron's spin frequency, orbital angular frequency and de Broglie wavelength (for bound electrons) or spin frequency (for free electrons), as well as rejecting quantum vacuum wavemodes of a longer wavelength than any given particle's diameter (much like a Casimir cavity does):
http://vixra.org/pdf/1203.0033v1.pdf
Proton and electron mass derived as the vacuum energy displaced by a Casimir cavity
"Two of the great mysteries of physics are the origin of mass and the mysterious mass ratio between the proton and electron of ~1836. In this paper it is shown that the mass-energy of the proton is equivalent to the vacuum energy excluded by a spherical Casimir cavity with an average radius equal to the charge radius of a proton. Likewise the electron mass is shown to be equivalent to the vacuum energy excluded by a spherical shell with an average diameter equal to the Compton wavelength of the electron. The ratio ~1836 is derived as a natural consequence of the vacuum energy exclusion."

For another instance, a Casimir cavity's walls reject quantum vacuum wavemodes which are outside the wall, leading to a lower quantum vacuum expectation value between the walls. Because of this rejection of wavemodes, there is a lower quantum vacuum field radiation pressure and thus space-time expands in the cavity, creating an energy "well". This manifests as a force pushing the walls of the Casimir cavity together (and interestingly, at <10nm cavity wall separation distances, the force is approximately equal to atmospheric pressure over the Casimir cavity wall area, even in a normal vacuum).

https://web.archive.org/web/20090228202428/http://physicsworld.com:80/cws/article/print/9747
"Although this force might appear small, at distances below a micrometre the Casimir force becomes the strongest force between two neutral objects. Indeed at separations of 10 nm - about a hundred times the typical size of an atom - the Casimir effect produces the equivalent of 1 atmosphere of pressure."

For another instance, our GPS satellites must account for being further outside the gravity well of our planet by adjusting their clocks to account for their faster time evolution (the 'deeper' in a gravity well one is, the slower time evolves, so the satellites being 'shallower' in our gravity well means time for the satellites evolves faster than time at the planet's surface). The satellites must also account for their motion causing their time evolution to slow down. The two effects don't completely cancel, so each must be accounted for. If they were not, the GPS satellites would give incorrect coordinates in as little as a day.

And we've got some research to corroborate the empirical examples:
https://arxiv.org/pdf/hep-ph/0603254.pdf
That's a PDF file entitled: "Negative Pressures in QED Vacuum in an External Magnetic Field". Scientists from Grupo de Fisica Teorica, Instituto de Cibernetica, Matematica y Fısica in Havana, Cuba did the research.
"A positive pressure is exerted in the direction parallel to B, while negative perpendicular to B pressures appear. This means that vacuum shrinks perpendicular to the magnetic field and freely flows parallel to it."
Rodriguez and Quertz got the sign wrong in their equations, thus it's a negative pressure exerted in the direction parallel to B, and a positive pressure perpendicular to B. Their results would be in direct contradiction to General Relativity, whereas a simple sign flip brings their results into agreement with GR.

https://pdfs.semanticscholar.org/1251/fea14a765b9c9289f8cf0206208bf49e0d8a.pdf
"While 'mass attraction' depends only on mutually attracting masses and their relative position or distance, G (a so-called, 'non-derivable constant') can be effectively derived and is found to be the exact inverse of 'vacuum mass density equivalent' (5.156e96 kg/m3), which is come to by dividing the Planck mass by the product of Planck volume and the square of Planck time (the former having already been predicted as an approximate value, e.g. in [3]). This new equation of gravitation resulting from the substitution of G by Planck units reveals that vacuum density (analogous to Zero Point Radiation [ZPR]) affects gravity inversely. This means that, if we were able to increase ZPR, gravity would decrease and vice-versa."
Magnets have this effect upon quantum vacuum zero point energy field radiation pressure, as described above. Thus magnets can increase stress-energy tensor to contract space and speed up time, and decrease stress-energy tensor to expand space and slow time down. So while magnets can affect space-time curvature, they aren't generating what we know as 'mass gravity', so we can't say magnets affect gravity... we can say that magnets have an effect upon space-time curvature in a similar vein as mass does.

http://www.pitt.edu/~mingchen/Research_papers/CGSY.071509.pdf
"Vortices arise as static solutions to gauge field equations in two-space dimensions. Unlike monopoles, magnetic vortices not only arise as theoretical constructs but also play important roles in areas such as superconductivity [1, 30, 37], electroweak theory [3, 4, 5, 6], and cosmology [81]. The mathematical existence and properties of such vortices have been well studied [7, 8, 9, 10, 25, 27, 37, 43, 44, 48, 50, 54, 55, 57, 65, 68, 69, 75, 86]. Naturally, it will be interesting and important to establish the existence of dyon-like vortices, simply called electrically charged vortices, carrying both electric and magnetic charges. Such dually charged vortices have applications in a wide range of areas including high-temperature superconductivity [40, 47], optics [11], the Bose–Einstein condensates [33, 39], the quantum Hall effect [66], and superfluids."

This paper tried to apply the temporally-infinite-base 4-D manifold of Minkowski space-time to their equations, as outlined on page 3, but a "nontrivial temporal component of the gauge field" frustrated their efforts, so they only considered the vortexes in our "snapshot" of time, in other words, static without considering temporal effects.

In Theorem 9.4, they postulate a multiplet of n − 1 Higgs fields each lying in the Cartan subalgebra of su(n) (ie: they extended their equations out over a finite-dimensional field to approximate the infinite temporal base field, to try to arrive at at least some form of temporally-inclusive solution), leading them to conclude that "such a magnetically and electrically charged solution realizes an SU(n) vortex configuration asymptotically and topologically represented by the mth integral class in the classification space of the vortex vacuum manifold", closing with "To conclude, in this paper, we have developed an existence theory for the electrically and magnetically charged vortex solutions arising in the classical Abelian and non-Abelian Chern–Simons–Higgs models using a constrained variational approach.".

Note the magnetic vortex seems "static" because magnetism stresses the QVZPE field density, and thus affects time... so the vortex appears to be static taken from the "snapshot" of our time frame... when in reality it is spiraling through time... the inflowing interface is spiraling out behind our time frame, whereas the outflowing interface is spiraling out ahead of our time frame. This is because virtual photons are not temporal particles, they are not locked to our frame of reference.

 

Prometheus posted this 25 September 2018

THE A FIELD
----------
"Ok, that explains the B field of a magnet, but what about the A field?", you may be asking. And that's another good question.

Essentially, the B field is an effect of the vector potential A field. Magnetic vector potential A is a polar vector, whereas the magnetic flux density B is a pseudovector. The curl of a polar vector is a pseudovector, and vice versa. B=curl(A). The pseudovector B field is equal to the rotational flow of the vector potential A field. The A field is due to the bound electron spin and orbital angular momentum, and the B field is the resultant magnetic field.

The magnetic vector potential field is the concept which allowed us to unify electric and magnetic fields. It is Faraday's 'electrotonic state' concept brought to mathematical fruition by James Clerk Maxwell, Faraday's successor (Faraday handed Maxwell all his research notes in 1855). Whereas the B field is magnetic flux density, the A field is magnetic vector potential. Whereas B has dimensions of electrokinetic momentum per area, A has dimensions of electrokinetic momentum per length.

This ties directly into magnetic induction... imagine a loop of wire in which current is running counterclockwise (we'll discount resistance for now). The Right-Hand Rule states that a B field will be manifested at a 90 degree angle to the direction of rotation of the current in the loop of wire, thereby the magnetic field will extend toward you. Now spin the loop of wire about its axis in a direction opposite to current flow. You'll note that as rotational speed increases, the B field strength decreases. The rotation is counteracting the vector potential A field by canceling its rotational flow (reducing its electrokinetic momentum per length) in 4-space. The rotation is canceling the curl (rotation) of the A field, thereby weakening the B field.

"How does the A field tie into the Aharonov-Bohm Effect?", you ask.

Consider two particles emitted along two different paths toward a common target. Upon being emitted, each particle's quantum mechanical wavefunction has a certain phase. Even if the wavefunction phases of the two particles were the same when they were emitted, their relative phase will change due to the difference in the paths taken. Thus, even if a magnetic field between the two particles is nonexistent, the electric field potential may not be. This is manifested as the Aharonov-Bohm Effect, where two particles can affect each other even if B=0 due to their quantum mechanical wavefunction phase shift.

Thus the magnetic vector potential A represents the phase shift per unit charge as those particles move through space. Note that the electric scalar potential is the phase shift per unit charge as a charged particle moves through time. So the magnetic vector potential bears the same relationship to space as the electric scalar potential bears to time. Thus the Aharanov-Bohm phase shift (observed when electrons pass a long solenoid which corresponds to a line of magnetic dipoles) is analogous to the Matteucci-Pozzi phase shift (observed when electrons pass a line of electric dipoles).

This is why the electric scalar potential constitutes the time component and the magnetic vector potential constitutes the space component of a Minkowski space four-vector (a four-vector is a four-dimensional vector representation of space-time with coordinates x (x coordinate), y (y coordinate), z (z coordinate) and t (time coordinate). It allows Lorentz transforms for all nongravitational physical phenomena).

Prometheus posted this 25 September 2018

APPLICATION
----------
The above can be applied to not only understand physical phenomena, but to conceive of new ways of exploiting those phenomena to build working devices which, for instance, generate electricity without requiring energy input, or reduce gravity via gravitoelectromagnetic coupling.

One application is the Spin Hall Effect.

In essence, by splitting the Charge Current into two Spin Currents (a current of moving spins without charge flow), one can create a vector force by the application of opposing magnetic fields to the Spin Currents.

Another applicaton is my triboelectric charge-separation motor idea, operating upon the same principle as the Searl device (but much simplified and more direct). It steals bound electron orbital momentum and uses it in attempting to conserve the angular momentum of the permanent magnetic field and the frame-dependent magnetic field, resulting in a unidirectional rotation. The bound electrons regain their usual orbital momentum by absorbing energy from the quantum vacuum. This device should also exhibit gravitoelectromagnetic coupling via a large electron accelerational change... gravitoelectromagnetic coupling is miniscule at low electron velocity, but a large rate of change of electron velocity implies a larger coupling coefficient. My triboelectric charge-separation motor idea utilizes such a large rate of change of electron velocity via a geometrical transform. This change of reference frame makes the electron transition from stationary (in the rotor's frame) / rotating (in the lab frame) to rotating in the opposite direction (in the rotor's frame) / stationary (in the lab frame). Gravity is a uniform acceleration, and it does distort a Coulomb field. Thus the inverse (an electron's acceleration distorting the gravitational field) should also take place.
http://www.aboveunity.com/thread/john-searl-self-generating-ring-and-roller-magnets-cold-electricity-inverse-gravity-flight/?order=all#comment-f53eac76-a5ce-4706-8748-a95d0027f985

Another application is spin-transfer torque, a spintronics application. Torque is simply the time rate of change of angular momentum. Spin-transfer torque arises whenever the flow of spin-angular momentum through a material is not constant. For instance, a magnet of a certain spin-dependent electron momentum density (spin current density) will exert a torque upon another non-collinear magnet of different spin current density (typically the magnets will be of different composition). The second magnet necessarily absorbs a portion of the spin angular momentum carried by the electron spins in the first magnet, exerting a torque. This phenomenon could, for instance, be used in a magnetic gearset to attain more energy output than was input, by stealing some of the first magnet's electrons' angular momentum. The electrons would then attain more energy from the quantum vacuum to normalize their angular momentum, as described above.

Alternatively, a magnetized ferromagnetic material will experience torque from itself when in the vicinity of an exceedingly thin metal (for instance, Cr/Fe, Cu/Co or Cu/Ni) via the process of spin filtering reflecting only certain wavefunction spin orientations back toward the magnet. One can view this effect as simply the precession of the spin in the exchange field of the magnet. This is harder to implement because the metal must be very thin or the path length through the metal will cause the A field (which, if you'll remember, is a measure of the phase change of a particle as it moves through space) to de-phase, causing the transverse spin angular momentum components of the spin vectors to average to zero. So the metal must be less than a few atomic lattice constants thick. So if Cr (chromium) were used, it'd have to be less than ~0.873 nm thick. For Cu (copper), it'd have to be less than ~1.085 nm thick. So this is more for MEMS applications.

Another application is motionless generation of electricity without energy input. By filtering the helicity of the virtual photons on each pole face of a magnet into two separate streams, we could stress the quantum vacuum, generating time imparity effects, which is how electrical generators work to begin with (the magnet's inflowing and outflowing interfaces on each pole face slow down and speed up time evolution respectively, but since they cancel out we must introduce the relativistic effects of motion to create the space-time compression and thus charge compression which generates current flow). Of course, we have no way of filtering virtual photons by helicity yet.

There are many more applications. One must only apply one's imagination and creativity to conceive of them.

Chris posted this 25 September 2018

Prometheus, WOW what a treasure trove of information!

Thank You!

   Chris

  • Liked by
  • solarlab
Vidura posted this 25 September 2018

Great información prometheus, although many things are beyond my understanding, and my knowledge in qm is very basic, I appreciate the way you can explain with simple examples and analogies.

  • Liked by
  • Chris
  • solarlab
Prometheus posted this 26 September 2018

Prometheus  ..  Obviously you are a degreed scientist, and one of the best, since you understand quantum physics. And that's very, very rare for a scientist to be open to the alternative "free" energy ideas. We are honored to have you here. Can we know your name and degrees?

Do you have the big downloads of Patrick Kelly and Robert Nelson?

I don't want to appear to criticize a man such as you, but I think you may find that Einstein's Relativity is faulty. For instance, it has become clear to many that the Big Bang never happened. And I can back that up. And the idea of mass increasing to infinity at the speed of light, can't be.

Chris, this is the ultimate on magnetism, and should be under your Magnetic Field topic.

No, I'm not a scientist... they don't get paid enough for the amount of work they do (those in the hard sciences, that is), and an inordinate amount of that work is finding and maintaining funding. I do have formal education in nuclear physics, but for the rest I'm autodidactic.

Yes, I have Patrick Kelly's PDF files (and 65.9 GB worth of other files I've read and archived for future reference). Unfortunately, Patrick Kelly now believes in flat earth, bringing into question his other conclusions. This doesn't, of course, affect the work of those he includes in his PDF files.

Of course the mass of an object  doesn't actually increase at relativistic speeds, as that would imply a change in the internal structure of that matter. What really happens is that the geometric properties of space-time around that relativistic-speed object change such that it appears as though the object increases in mass.

{EDIT}

I'm putting this here for future reference:

http://intalek.com/Index/Projects/Research/FundamentalNatureOfRelativisticMassAndMagneticField.htm

Topics 5 and 6 show that relativistic increase in mass is merely the mass-energy (mass-momentum) equivalency increase in the energy of the magnetic field of a relativistically-moving charged particle. Given that all invariant-mass matter is comprised at least partially (excluding neutrons) of charged particles, and given that even neutrons are comprised of quarks (which each carry partial charge - up quark: +2/3, down quark: -1/3) this accounts for the relativistic increase in mass of all matter.

{/EDIT}

Einstein's Special Relativity has been tested literally thousands of times via literally thousands of different avenues, and it's never come up lacking. The same cannot be said of General Relativity (it's been tested, but not to the extent of SR), so one must be sure not to confuse the two. What has come up lacking is people's understanding of the concept, which led some people (even scientists in Einstein's day) down the primrose path of mysticism... some of them were using SR (and GR) to claim the universe 'deconstructed' all matter that an intelligent being wasn't directly observing, which would imply an intelligent universe, instantaneous action at a distance and thus irredeemably broken causality.

As for the Big Bang, a big clue could be had from the shape of the universe. Unfortunately, the universe is so large that we can't see beyond our cosmological particle horizon (although I suspect the CMB is merely the 'funhouse mirror' optical surface of the red-shifted light from beyond our cosmological particle horizon), so we can detect little curvature. But the anisotropy in the CMB (first seen via the Wilkinson Microwave Anisotropy Probe satellite) points to the universe being finite and anisotropic (the longest CMB wavelengths are missing... likely because the universe is simply too small to sustain those vibrations).

I suspect it's a 3-Torus, but have nothing to back that up except that a 3-Torus is topologically flat just like our universe, although topologically flat doesn't necessarily imply actually flat (a flat surface can be rolled into a cylinder, and that cylinder shaped into a torus, so a flat surface and a torus are topologically isomorphic), and that's a pretty ubiquitous shape in our universe (a magnetic dipole, for instance).

https://arxiv.org/pdf/astro-ph/0302496.pdf

https://www.nytimes.com/2003/03/11/science/universe-as-doughnut-new-data-new-debate.html

  • Liked by
  • Chris
  • solarlab
Prometheus posted this 26 September 2018

Prometheus   ...  I don't think I'll ever understand much of that.

Can you tell us? Is there something real flowing around a magnet and between magnets, a magnetic current?

And I see you believe there's a Bloch Wall in a permanent magnet. Do you agree with the double torus shape, rather than one torus of a magnet?

Yes, there is. Virtual photons. As you know, photons are the force-carrying bosons for the EM fundamental force.

The proper way of stating it is that photons mediate the EM interaction, and virtual photons mediate magnetism.

As explicated above, the magnetic dipole can be considered a double torus. But for a typical permanent magnet, it's only a "double torus" (or, more accurately, two intermeshed vortexes) because of the intrinsic magnetic softness of our materials. We'd need to increase magnetic hardness by at least an order of magnitude to get a magnet with all domains kept perfectly aligned unidirectionally, and we simply don't have the material to do that yet.

As for the Bloch Wall, you can use magnetic viewing film to see it in any typical magnet. There will be a bright line at the midline of the magnet because magnetic flux parallel to the viewing film makes the nickel flakes orient their reflective face such that external light is reflected, giving a bright line. Thus the canted domains at the Bloch Wall are out of alignment with the two predominant magnetic directions.

 

  • Liked by
  • Chris
Aetherholic posted this 26 September 2018

Sorry to disagree, there is no such thing as a virtual photon just as there is no such thing as a photon. A magnet is a coherent dielectric object constraining aether energy transfer to be substantially planar within the material.

Aetherholic - One truth, One field

  • Liked by
  • Chris
Chris posted this 26 September 2018

Hey Aetherholic,

Nothing wrong with that, to Gentlemanly Disagree!

It took me some time to understand the meaning of the: "Virtual Photon Flux"

CEM, classical electromagnetics, is still utilizing a model based on a material ether. Although the Michelson-Morley experiment destroyed the material ether assumption in 1887, the classical electromagnetic model has never been corrected. It also contains no definition of charge, and no definition of potential. In many cases, algorithms to calculate a magnitude are boldfacedly and erroneously advanced as "definitions." CEM, classical electromagnetics, still prescribes the force fields as the causes of all electromagnetic phenomena; it has been known since 1959 that forces are effects and not causes, that electromagnetic force fields exist only in and on the charged particles of mass in the physical system, and that the potentials are the primary causes of electromagnetic phenomena.

The lack of definitive definitions of mass and force in mechanics is carried over into electromagnetic theory; there is no adequate definition of electromagnetic force or of electromagnetic mass. The magnitude of the electrical charge on an electron is not quantized. Instead, it is discretized, being a function of the magnitude of the virtual photon flux) (VPF) exchange between the vacuum and the charged particle. When the charged particle is placed in a potential that differs from ambient, then the magnitude of the virtual photon flux) (VPF) - and hence the magnitude of the electric charge on the electron - is altered.

The CEM, classical electromagnetics, assumption of an "empty vacuum" is totally falsified by modern quantum mechanics. The CEM, classical electromagnetics, notion that electromagnetic force fields and force field waves exist in vacuum is totally false. Only potentials and potential gradients exist in the vacuum. Electromagnetic waves in vacuum are not force field waves as CEM, classical electromagnetics, prescribes; instead, they are oscillations of potentials and potential gradients.

Potentials have a bidirectional electromagnetic wave-pair structure, where the bidirectional wave pairs are phaselocked in a harmonic series. In each wave pair, photons and antiphotons are continually coupling (into spin-2 gravitons) and decoupling. This is where gravitation and electromagnetics are unified. The CEM, classical electromagnetics, notion that singular electromagnetic forces exist in either matter or the vacuum is false; Newton's third law requires that all forces exist in oppositive pairs.

Ref: http://www.svpwiki.com/virtual+photon+flux

 

Now, for me, my understanding, in an Electric Universe, where the majority of the building blocks of Nature have Charge and as a result a Magnetic Moment, "Virtual Photon Flux" simply is the Aether, a Fluidic Medium where Energy is transferred, The Quintessence. Invent one Term to replace the other Term with the same thing.

That's just my opinion, Science cant say Aether. I am a firm believer in Science but I do think we have made some mistakes.

We Humans have so much to learn, so much to correct, Smart people can not learn if they think they know everything!


@Bob, I am not the "ultimate on magnetism", I am sharing my results, what I have learnt, observed and studied, I have a long way to go, but am more than happy to move forward...

 

 

 

 

 

 

 

:

 

Yes, I have seen what Prometheus describes. I have covered some data in: The Field Structure of Nature and Magnetic Field Observations.

   Chris

Chris posted this 26 September 2018

Worth a new post:

I hope we all caught the use of:

Potentials have a bidirectional electromagnetic wave-pair structure

 

Which, by definition, is a Standing Wave:

 

 

 

So, the Virtual Photon Flux is, because we saw in the above definition, Potentials and Charge, is, Standing Waves.

We have data that the Electron is, or at least has a Standing Wave Structure and when resonant, is seen:

Ref: http://www.human-resonance.org/electron.html

Ref: https://physics.aps.org/story/v21/st7

I quote the article:

The quantum stroboscope's images of the electron are a first glimpse into the subatomic realm. The nonlinear concentric rings comprising the electron's structure display the unmistakable Fibonacci order expressed in the quadratic function [ zn+1 = zn2 modulus n ], pictured above. This sacred mathematical structure is reflected as a standing wave pattern of resonance existing on all scales of the cosmos, in individual electrons, in crystals of calcite, in giant pyramids, all planetary bodies, and even underlying the form of galaxies.

 

My Friends, I have said it before, although this article is 10 years old, we are still Light Years ahead of the rest!

   Chris

  • Liked by
  • cd_sharp
Aetherholic posted this 26 September 2018

Chris

I would normally stay quiet but I do care about such well intentioned people here being led down the same dead ends. Just a few last points then I will shut up again for a while!

The aether has absolutely nothing to do with virtual or any other photons. It is a resonant system that resides way below the planck length at 10^-50. Very simple mathematics can be used to model it and derive every known physical constant and phenomena and many that are unknown to the mainstream at present. Whilst Ken Wheeler doesnt go into what the aether is, I suggest anyone that has discounted what he says regarding light and magnetism should take a second look. In this regard I do know what I am talking about as I have patents and products which use some of the magnetic and dielectric properties he describes, were designed with theory and worked first time with no development.

The evidence for gravity being non-coherent dielectric acceleration is strong. There is a paper published where one of the components in the planetary motion equations was replaced with cross sectional area. This increased the calculation accuracy. I think it was the person who helped Nassim Haramein with his Scaling Law paper. The implication that the gravitational acceleration is primarily an area effect has obvious implications.

So, when considering phenomena, if you keep in mind that everything that is observed is a second or third order effect resulting from a single resonant systems boundary interactions then in my opinion this is the correct path.

Enough controversy for now, back to finishing the Figuera device!

Aetherholic - One truth, One field

  • Liked by
  • Chris
Chris posted this 26 September 2018

Hey Aetherholic,

Hahaha, I think we just agreed, post for post, we have identical data, only a few seconds apart.

   Chris

  • Liked by
  • Aetherholic
Prometheus posted this 26 September 2018

Prometheus   ..  A degree in nuclear physics, you are a scientist. Alright, you self-learned more about the quantum. I think you are more of a genius than you think.

"As you know, bosons.."  No, I don't know quantum physics. I've heard the ideas said, but I only understand quantum by the philosophy of Ying-Yang. Each particle must have it's opposite, positrons and electrons, etc. I prefer Walter Russell's explanations.

I've come to the conclusion that there is no strong force. An atom is like a permanent magnet. There is no strong force holding it together. If you break a magnet then you can't put the pieces back together because they repel each other. One unit no longer exists.

We have covered the Bloch Wall in the Magnetic Field Topic. I said what you have said about the orientation of the magnet film. I think it is a light line because the two poles are exactly equal there. I don't think it's a domain wall because if you add another magnet the light line changes to the midline of the two magnets. Hard fixed metal domains could not shift like that.

You have a misunderstanding of what domains are... just because a magnet is made of hard metal doesn't necessarily imply that it has a high magnetic hardness (which is a measure of a magnet's ability to resist electron spin flipping). The domains flip in externally-stressed magnets, and in fact your examples above (stacking two magnets, breaking a magnet) shows this to be true. Most stressed magnets which are made of crystallographic anisotropic material will flip back once the stress is removed.

As an exercise, place a sensitive microphone on a magnet and connect it to an amplifier. Then bring another magnet near the first magnet. As the two magnets get closer and closer, you'll hear a crackling noise in the speakers connected to the amplifier. This is known as Barkhausen noise, and it is the electron spins flipping and thus the domains rearranging.

The strong force doesn't hold the atom together, it holds quarks together to make protons and neutrons, and it holds neutrons and protons together to make nuclei via exchange of gluons (the force-carrying bosons which mediate the strong force).

Nowadays, the strong force is usually called the color force, but diving into Quantum Chromodynamics (which has nothing to do with actual color, and is instead about a type of charge) can be head-spinningly confusing for neophytes, so I used the older terminology. The strong force term was coined before we knew about quarks and gluons.

It cannot be the EM interaction holding a proton together, for instance... the EM interaction has two charges (+, -), whereas the strong force has three charges (red, green, blue).

Physicists had to call the charges something, so they settled upon red, green and blue... so a stable nucleon is considered "white" (the color charges mutually cancel).

  • Liked by
  • Chris
Aetherholic posted this 26 September 2018

@Idea1man

I will start a new thread for this after I have finished the Figuera project as the particular application and research has many implications for different science disciplines apart from magnetic phenomena. 

As for products, which I am NOT here to sell, if you really want to know I will post a link in the new thread AFTER I have discussed the technology, which is related to the magnetic and dielectric fields, so I wont get accused of trying to sell something.

Aetherholic - One truth, One field

  • Liked by
  • Chris
Prometheus posted this 26 September 2018

Sorry to disagree, there is no such thing as a virtual photon just as there is no such thing as a photon. A magnet is a coherent dielectric object constraining aether energy transfer to be substantially planar within the material.

 

Chalmers University in 2011 concretized real photons from the virtual photons in the quantum vacuum using a SQUID (Superconducting Quantum Interference Device). All they did was mimic the process by which virtual photons very briefly pop into existence (the difference between concretized and virtual particles is that virtual particles are a result of an unstable perturbation in the quantum vacuum, and they therefore 'smear out' their energy back into the quantum vacuum so quickly that we can't observe them).

Add enough energy (or have that energy otherwise available) and you can concretize virtual particles into real particles (pair production from the quantum vacuum in a high field strength environment, which happens around magnetars). Add enough energy and set up the proper standing wave within the Higgs field, and you can concretize any type of matter from the quantum vacuum.

This is how the 3-photon experiment worked... the three photons had enough energy inherent to them that when they were fired through a rubidium Bose-Einstein condensate, the three photons entangled and set up a standing wave in the Higgs field, lending the photons mass... the researchers called it photonic mass, but it was matter (it had invariant mass, and traveled slower than c). This was the very first time humanity had converted energy to mass (we've known for a long time how to convert mass to energy). It's the very first baby step toward a Star Trek-type replicator, able to produce any matter at will from the quantum vacuum.

 

  • Liked by
  • Chris
Aetherholic posted this 27 September 2018

In my opinion

The difference between the aether and the QM "soup" is that QM believes in total chaos causing spontaneous emission from bumping virtual particles where as the aether is a resonant system in equilibrium with no chaos and very predictable phenomena. The two could not be more different. The strong force is dielectric acceleration, the same as is the weak force, the same as is gravity.

Aetherholic - One truth, One field

  • Liked by
  • Chris
Prometheus posted this 27 September 2018

Thank you, Prometheus, for educating me. I haven't heard of the terms you mentioned, like magnetic hardness. I did hear about the noise approaching a magnet, if amplified. Someone, maybe Eric Dollard, said the scratching noise proves there are magnetic lines of force.

I don't bother reading about quantum particles. I'm not interested in it, and don't have the time for it. Scientists are already mistaken about so much, I don't want to learn more mistakes. I know the Strong Force is said to hold the nucleus together. But scientist merely dream that it must exist. They haven't found anything that I know of. Then they merely dream another particle is doing it, and call that the "glue", gluons.

What I think they need to do is go back to the correct way, by admitting that the quantum level is the Ether, and thus regain what was lost.

We know the strong force exists because it is what powers our nuclear weapons (and our nuclear power plants). The binding force released during the nuclear reactions is what creates the explosion and the heat to generate steam to generate electricity.

We know it can't be the EM force holding protons and neutrons together into nuclei, because the neutron is neutrally-charged.

The strong force was found by continually searching for smaller parts of supposedly "fundamental" particles via massive amounts of empirical experimentation in successively higher-energy colliders.

In the process, we discovered the underlying structure of atoms via mathematical reconstruction after a collision. To date, the mathematics is accurate to better than 1 part in 1 billion, and is still improving.

We've finally gotten to the point where we can't really subdivide the particles anymore, so quarks, gluons and electrons are fundamental.

Of course, Quantum Field Theory is coming up fast, and that equates energy and mass such that there are NO fundamental particles because all invariant-mass matter is actually standing waves within the Higgs field. And standing waves can be taken out of resonance, so even the supposedly 'fundamental' particles could be unwound into energy.

I have an idea for such a device, but considering the ramifications, it's best not developed... it'd make even the highest-yield atomic weapon look like a party popper, and would fit in a briefcase.

  • Liked by
  • Chris
Prometheus posted this 27 September 2018

In my opinion

The difference between the aether and the QM "soup" is that QM believes in total chaos causing spontaneous emission from bumping virtual particles where as the aether is a resonant system in equilibrium with no chaos and very predictable phenomena. The two could not be more different. The strong force is dielectric acceleration, the same as is the weak force, the same as is gravity.

If you're referring to Ken Wheeler's 'dielectricity', he's merely redefined static electricity (while denying that electrons exist). Static electricity under acceleration is an electrical current flow. So he's stating that what we term the Bloch Wall (his 'dielectric inertial plane', where he's redefined dielectricity to mean static electricity and inertia to mean 'the opposite of rest' and therefore motion) has a current flow. We know it doesn't (except for the electron orbitals, but that also happens throughout the magnet).

And you're stating that gravity is therefore also electrical current flow. That doesn't work because Wheeler's theory doesn't work, which is why it's been debunked via more than 30 different avenues on overunity.com. I've read Wheeler's book, and I understand it, which is why it was so easy for me to poke a plethora of holes in his theory.

Magnets are not 'dielectric' (especially when dielectricity is redefined), we already have a scientific description encompassing an explanation: ferromagnet.

Lest we veer off into having to (yet again) debunk Wheeler's hobby theory (which will likely get the thread locked), I propose you study what I've written above and the included references. When you understand how the universe works, you'll also understand that a Wheeleric Universe could not exist.

 

  • Liked by
  • Chris
Aetherholic posted this 27 September 2018

Prometheus

Thats fine, we will agree to disagree, if you think that a dielectric field is static electricity thats fine too, and if you think that overunity.com is the bible for information thats fine also. I have data that says I am correct and I am fine with that. Everyone is entitled to their own view of the universe, I am just sharing information that I have verified to myself as correct, its entirely your prerogative to decide what you do with it. 

Aetherholic - One truth, One field

  • Liked by
  • Chris
Prometheus posted this 28 September 2018

Prometheus

Thats fine, we will agree to disagree, if you think that a dielectric field is static electricity thats fine too, and if you think that overunity.com is the bible for information thats fine also. I have data that says I am correct and I am fine with that. Everyone is entitled to their own view of the universe, I am just sharing information that I have verified to myself as correct, its entirely your prerogative to decide what you do with it. 

It's not whether I think that Wheeler's 'dielectric field' is merely an electrostatic field, it's that Wheeler has explicitly stated same.

Specifically, his statements on overunity.com:

"YOU TELL ME how I can CHARGE a  "non-conductive" piece of GLASS with enough DIELECTRIC (electrostatic) charge to STOP A PERSONS heart?"

And:

"natures NATURAL 'electricity' isnt electricity at all, its DIelectricity."

So he's redefined static electricity as 'dielectricity'.

Further, in his book, he specifically states that the opposite of inertia is rest:

"Contrary to empirical phenomena and objects which are in motion and are denoted to have ‘inertia’ and likewise its opposite being ‘rest’."

Objects in motion are denoted to have 'inertia'... but then, so are objects at rest. What an object at rest does not have is momentum, which is a means of measuring that object's motion.

The opposite of "rest" is not "inertia", as an object has inertia whether it is at rest or it is moving (inertia being defined as the tendency to resist changes in an object's state of motion, even if that 'state of motion' is the state of being at rest)... the opposite of "rest" is "motion", quantified via "momentum"... one would think this would be obvious.

Inertia doesn't really have an inverse, it's not a transferable property... when you push on an object, you don't impart any inertia to it nor receive any inertia from it. The only time an object's inertia changes is when the mass of that object changes, for massive objects.

For massless entities, given that energy and momentum are proportional (E2 = p2c2 + m2c4), the only time a massless entity's inertia changes is when the frequency of that entity changes or the direction of that entity changes... the energy-momentum equivalency for massless entities is the reason black holes were predicted to exist before we actually empirically observed any, why gravity can bend light (gravitational lensing), and why light under the influence of gravity changes frequency (blue-shifts as it goes down the slope of a gravity well, red-shifts at it climbs out of that gravity well).

So Wheeler's 'dielectric inertial plane' using Wheeler's own redefinitions means he must be speaking about "static electricity in motion"... an electrical current. And we know the Bloch Wall of a magnet does not have any electrical current (again, besides the orbiting electrons, but that happens throughout the magnet).

Wheeler's theory doesn't fit the facts, thus it cannot reflect reality. He pilfered a bunch of terms from Circlon Theory, Russellian Theory, Dollardian Theory and a few other hobby theories (then claimed discoverer status) and attempted to patchwork them into a workable description of the universe... but it doesn't work, and would result in a universe which could not exist.

  • Liked by
  • Chris
Chris posted this 28 September 2018

@All - Please, no more on Ken Wheeler.

We all have our opinions, much of the time our opinions are a different way of looking at the same thing.

Lets focus on Topic, not get distracted!

@Prometheus - The Black Hole, is the absorbed Mass entirely eject from the Jets? What's the In to Out ratio? Has Science measured this yet?

   Chris

 

P.S: Why do we see two jets from Black Holes, not one?

  • Liked by
  • Vasile
Prometheus posted this 28 September 2018

The accretion disk and astrophysical jet around a black hole (active galactic nuclei) is merely the process which results from the mass of the black hole so distorting space-time that the infalling accretion flow spirals in. This is a result of frame-dragging by the black hole. This spiraling generates a magnetic field (the first thing to get ripped away from atoms in that strong of a gravitational field is the electrons, so the infalling matter is ionized... rotating charge generates a magnetic field), and that magnetic field imparts enough energy to some of the infalling matter to propel it away aligned with the magnetic field.

Under the right conditions, the matter ejected in the jet can collimate, which allows the jet to traverse vast distances before the beam deionizes, via the same mechanism used in PrOCSIMA (Photon-particle Optically Coupled Soliton Interstellar Mission Accelerator).

The electrons and ionized matter are beamed along the magnetic field lines, interacting via their magnetic and electric fields, creating a JxB interaction force which causes the beams of electrons and ionized matter to spiral around each other, so the overall beam doesn't diverge very much (the jet can extend for millions of parsecs... so millions of trillions of miles. That sounds like a lot until you consider that the observable universe out to our cosmological particle horizon is ~550 septillion miles across, or 550 trillion trillion miles.). Eventually, the electrons will again be captured by the matter, whereupon the beam scatters.

Accretion disks only exist just outside the event horizon of approximately 1% of black holes, and only about 10% of those have astrophysical jets, so it's a pretty rare phenomenon. This is because it's a balance between the radiation pressure from the infalling matter (which is dependent upon the amount of  infalling matter) and the gravitational force of the black hole... too much matter infalls and the radiation pressure exceeds the gravitational force, blowing the material outward and shutting off the jet (at least, until that matter infalls again). Too little radiation pressure and the gravitational force sucks the matter into the black hole without forming a jet.

This is a dynamic process, changing on the order of mere hours. It creates shock collisions as the pulsating jet ejects more matter, then ejects less matter, then more, etc.

Thus, it's impossible to give a single number for the ratio of infall to ejecta.

  • Liked by
  • Chris
Chris posted this 28 September 2018

Hey Prometheus,

Well, I have visions of an Ion Engine right now. Of course with only one Jet, not two.

 

   Chris

Prometheus posted this 28 September 2018

Well, the astrophysical jets are magnetic in nature, so there has to be two jets (typically, the positively-charged and negatively-charged ions are ejected in opposite directions, but there is entrained oppositely-charged matter in both jets, which is why they collimate)... but that's not to say that a device operating on the same principles (a tightly-spiraled magnetic field can accelerate charged particles to relativistic speeds in a collimated beam) can't have both jets aimed in the same direction such that they intermesh to mimic an astrophysical jet.

Imagine a scoop at the front of such a device, scooping up particles, whereupon they're ionized (perhaps in a strong radiation field?) and ejected by the spinning magnetic field of a rapidly-spinning permanent magnet assembly into two beams which are intermeshed. That'd provide a collimated beam of magnetism and charged particles which would provide additive thrust (the longer it runs, the longer the 'trail' of collimated beam is, and it's all pushing against the craft. The only energy input necessary would be the motor to spin the magnet and the radioactive material.

Now utilize the spin density differential concept to create that spinning magnetic field from stationary permanent magnets. The only energy input would be the radioactive material to ionize the particles. It'd make for pretty efficient propulsion of a spacecraft. With the right radioactive material, it'd last a long time, too.

 

  • Liked by
  • Chris
Prometheus posted this 01 October 2018

The magnetic powder is typically aligned in an external magnetic field so all the crystallographic easy axes are aligned. The field is maintained and the temperature is brought up as the powder is pressed and sintered above its Curie temperature. The external field intensity is increased to saturate the magnetic material, and the magnet is cooled while still in the external field.

Thus the crystallographic anisotropy (which strives for thinner or nonexistent domain walls and alignment along the easy axes) prevails because the external field is adding energy to the magnet. When that external field is removed, the exchange force can minimize internal energy, which is when the domains flip, starting at the pole faces and spreading through the bulk of the magnet, meeting at the midline to form the Bloch Wall.

So right now, we can't get that 'perfect' magnet... we don't have the materials to do so. We'd have to have at least 10 times the magnetic hardness of the hardest material available.

  • Liked by
  • Chris
Prometheus posted this 05 October 2018

Just so everyone is thinking about magnets from the proper perspective, the B field is an improper isometry reflection (rotoreflection) of the induced vector potential A field {B=curl(A)}, which is set up via an external magnetic field (ie: during magnetization). When that external field is removed, the exchange interaction causes what is essentially a 'reflection' of the predominant magnetic moment to minimize the magnet's internal energy, by flipping domains.

So we have a vector (the induced vector potential A field (Ainduced)), a pseudovector (the rotoreflected B field... Brotoreflected=curl(Ainduced)), a pseudovector of that pseudovector, the reflected B field (Breflected ≅ Brotoreflected, which isn't a vector because it's a similarity transform (a flipping of domains) rather than a rotoreflection) and a vector (the rotoreflected vector potential A field... Arotoreflected=curl(Breflected)).

This is why we don't usually sense or see evidence of the vector potential A field exterior to the magnet (barring any anisotropies in the crystalline lattice of the magnetic material) except when relative motion is introduced... in actuality, there are two vector potential A fields (Ainduced and Arotoreflected) and in a stationary frame with the magnet as the inertial reference frame, they cancel exterior to the magnet... but in a moving frame with the magnet as the inertial reference frame, they don't (which is why they don't cancel interior to the magnet in the moving frame of the bound electrons, which is how the magnetic field is sustained through time).

The above is why and how we get the Aharonov-Bohm Effect.

 

  • Liked by
  • Chris
Chris posted this 05 October 2018

Hey Prometheus,

I have studied the AB Effect to some degree, but in my time it appears to have some confusion surrounding it.

If you were to sum it up in a sentence, describe it in some detail for some that do not have great understanding of the AB Effect, how would you sum it up?

   Chris

Prometheus posted this 05 October 2018

It's a motion-induced phase shift between Ainduced and Arotoreflected, an exemplary example of Special Relativity's time-dilation, length-contraction effects of relative motion.

  • Liked by
  • Chris
Chris posted this 05 October 2018

Hi Prometheus,

I think many still would perhaps not understand.

I quote from my favorite article:

The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes and the particle's wavefunction being negligible inside the solenoid. This phase shift has been observed experimentally.

What's left behind when we enclose the Magnetic Field B inside a Core material, yes, the Magnetic A Vector Potential:

 

 

A Charge moving in, toward the Magnetic A Vector Potential experiences a Force via the Electromagnetic Force.

Now, if B is changing in Time ( ΔΦ some might be more familiar with δφ or dPhi ) and thus the Magnetic A Vector Potential is also changing in Time, then the Charge can be stationary, and thus experience the same Force!

Question: If the Magnetic Field B, is equal to Curl A, then what's A? Is it an Electric Field that all Charged Particles emit due to their Motion? Weather it be Orbital or Induced.

Why is a Permanent Magnet a Permanent Magnet? Should we call it a Permanent Electric-Field instead?

Vince posted perhaps the best image I have seen:

Magnetic flux exiting, or entering magnet.

 

Which follows the simple Ferro-Fluid experiment:

 

And also, Thomson's Model of the Electron Configuration:

 

   Chris

Prometheus posted this 05 January 2019

Sorry to take so  long to respond, I didn't see your response, then took time so I could answer as accurately as possible.

Using the image you posted above:

A beam fired toward an infinitely-long solenoid (which shouldn't have a magnetic field external to it) or toward a toroidal solenoid (which again, shouldn't have a magnetic field external to it) such that the beam is split toward either side of that solenoid, the two parts of the beam will experience different phase shifts as a result of the beam's motion relative to the aggregate sum of Ainduced and Arotoreflected  (which have opposite vectors) on either side of the solenoid.

One half of the beam will have its phase advanced, the other half of the beam will have its phase retarded. The phase shift will be a multiple of π, a consequence of flux quantization proportional to hc/2e.

"But if Ainduced and Arotoreflected have an aggregate sum of zero, then both beams should have their phases shifted equally regardless of their direction of motion within the vector potential A field, shouldn't they?", you may ask.

Well, yes, but you also have to take into consideration the helicity of the beam... the beam's "particle's" (either photons or actual particles) helicity will only interact with the A vector potential which has a similar helicity.

Of course, controversy surrounds the Aharonov-Bohm effect (and associated Matteucci-Pozzi effect, which has an associated semi-classical effect explanation). Timothy Boyer makes a credible claim that the effect is a result of the physicists (especially Akira Tonomura's team at Hitachi) not knowing that the niobium and copper shielding they used to purportedly block all magnetic and electric field effects outside their toroidal solenoid didn't actually block all magnetic effects, because "most physicists are unaware that magnetic velocity fields penetrate conducting ohmic materials in a fashion which is completely different from the skin-depth penetration of electromagnetic wave fields".

http://www-f1.ijs.si/~ramsak/seminarji/alic.pdf

http://cds.cern.ch/record/509771/files/0107099.pdf

In other words, you can't block magnetic fields, you can only divert them, as explicated by the corollary to Gauss's Law for Magnetism, which states "Magnetic field-lines always form closed loops.", and in so doing, you force the magnetic field to generate an associated electric field.

The electric field equivalent to the above is that electric field-lines begin on positive charges and end on negative charges, and never form closed loops. The work done in taking an electric charge around a closed loop is always zero. But you'll note that this only holds true for electric fields generated by stationary charges.

In the Aharanov-Bohm effect (and Matteucci-Pozzi effect), there is relative motion, so that leads to misinterpretation of the results, just as misinterpretation of the Double-Slit experiments as a result of state changes we introduced in measuring system state (Heisenberg's Uncertainty Principle) led us to believe that photons were both waves and particles, leading to the Wave-Particle Duality nonsense. Recent experiments which used a less-intrusive means of measuring system state (and thus didn't change system state as much) proved that photons are waves.

So it's going to require experiments with far more stringent parameters to resolve the A-B and M-P issue.

 

  • Liked by
  • Chris
  • cd_sharp
Chris posted this 05 January 2019

Hey Prometheus,

Soon to be known as the basis for Force Field Technology in the close future.

An excellent explanation, thank you!

   Chris

We're Light Years Ahead!
Our Above Unity Machines:

Asymmetrical EMI

Wistiti's Bucking Joule Thief
Non-Inductive Coil Experiment
CD's Non-Inductive Coil Rep
Baerndorfer's Experiment
Captainloz's A-R-E
Aetherholic's COP>4.0

Resonant EMI

Yo's Ferro Resonance
Jagau's Non-linear Resonance
Ferrite at work
Recomended Protocol:
Measurement
Switching System
Measurement Block
Current Observation
Current Sensing Resolution
Members Online:

No one online at the moment

What is a Scalar:

In physics, scalars are physical quantities that are unaffected by changes to a vector space basis. Scalars are often accompanied by units of measurement, as in "10 cm". Examples of scalar quantities are mass, distance, charge, volume, time, speed, and the magnitude of physical vectors in general.

You need to forget the Non-Sense that some spout with out knowing the actual Definition of the word Scalar! Some people talk absolute Bull Sh*t!

The pressure P in the formula P = pgh, pgh is a scalar that tells you the amount of this squashing force per unit area in a fluid.

A Scalar, having both direction and magnitude, can be anything! The Magnetic Field, a Charge moving, yet some Numb Nuts think it means Magic Science!

Start Here:
Help with using the Forum.
Message from God:

Hello my children. This is Yahweh, the one true Lord. You have found creation's secret. Now share it peacefully with the world.

Ref: Message from God written inside the Human Genome

God be in my head, and in my thinking.

God be in my eyes, and in my looking.

God be in my mouth, and in my speaking.

Oh, God be in my heart, and in my understanding.

Your Support:

More than anything else, your contributions to this forum are most important! We are trying to actively get all visitors involved, but we do only have a few main contributors, which are very much appreciated! If you would like to see more pages with more detailed experiments and answers, perhaps a contribution of another type maybe possible:

PayPal De-Platformed me!

They REFUSE to tell me why!

We now use Wise!

Donate
Use E-Mail: Chris at aboveunity.com

The content I am sharing is not only unique, but is changing the world as we know it! Please Support Us!

Thank You So Much!

Browse by Category:
Weeks High Earners:
The great Nikola Tesla:

Ere many generations pass, our machinery will be driven by a power obtainable at any point of the universe. This idea is not novel. Men have been led to it long ago by instinct or reason. It has been expressed in many ways, and in many places, in the history of old and new. We find it in the delightful myth of Antheus, who drives power from the earth; we find it among the subtle speculations of one of your splendid mathematicians, and in many hints and statements of thinkers of the present time. Throughout space there is energy. Is this energy static or kinetic? If static, our hopes are in vain; if kinetic - and this we know it is for certain - then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.

Experiments With Alternate Currents Of High Potential And High Frequency (February 1892).

Close