Melnichenko's Effect

  • Topic Is Sticky
  • Topic Is Locked
  • 13K Views
  • Last Post 07 November 2022
Jagau posted this 15 February 2022

Andrey Melnichenko is another great inventor and has several patents on the effect he found. On his Utube channel he made countless videos to demonstrate the effect he found.
Chris has made several demonstrations to allow everyone to better understand the different effects of Andrey Melnichenko's research and I would like to make it a study and continuity of his thread.
When doing various searches on the web it is very rare to find those who have managed to make a replica of its effect.
To study the phenomenon take the very simple diagram from the website of A. Melnichenko

This schematic has two coils L1 and L2 in mutual connection and as can be noted the same phase polarity (dot). To understand what is happening in the coils, an analysis of the polarities is necessary.
As Melnichenko himself explains there are two phases to take into consideration, the 1st magnetization and the 2nd demagnetization.
1 When magnetizing, T1 closes and L1 becomes negative on the bottom and positive on the top with the same phase polarities on L2. D1 and D2 being in reverse polarity then X1 and X2 do not light up.

 


2 During demagnetization, T1 opens causing L1 and L2 to reverse polarity as shown in the following diagram:



Since D1 and D2 are now forward biased then both diodes conduct so that X1 and X2 turn on.

Practical experience will follow to demonstrate if this is indeed what is happening.

Jagau

 

Order By: Standard | Newest | Votes
Jagau posted this 02 May 2022

My experiments on this phenomenon are at the beginning and I believe to have good results.   Is it possible to make Lenz Law non-existing, I believe melnicehnko solved some of this problem by making a nonlinear transformer this way:

The primary is air core and the secondary is ferromagnetic, nothing new yet but with an air gap between the two the output does not affect the input.

I would explain the Melnichenko effect this way: Lenz's law is almost non-existent or negligible because we use this type of non-linear transformer arrangement as there is no load connected to the secondary (idle).
The load is only connected in the demagnetization phase to the secondary.   
Read this you will understand what I mean in the principle of Melnichenko
https://www.physicsclassroom.com/class/waves/Lesson-2/Energy-Transport-and-the-Amplitude-of-a-Wave

For other questions about Lenz's law, I invite you to follow this demo by Professor Walter Levine from MIT, you will have your answers well explained

 Jagau

  • Liked by
  • Augenblick
  • Mimo
baerndorfer posted this 02 May 2022

yes melnichenko uses 2 e-cores seperated by air-gap and showed, that there is more energy in the whole system. this is fact.

but when you know what he did and when you know what POC can do. why not combining both ideas?

have a great day!

i do not want do destroy your thread - peace!

baerndorfer posted this 02 May 2022

hi jagau,

can you point out where the tesla patent describes the effect from melnichenko?

i studied this thing couple of times but canot find a link to andrej.

do you think, that shielding a coil with a magnetic circuit has the same effect as we can see on the 2 e-cores?

have a nice day!

  • Liked by
  • Jagau
  • Augenblick
baerndorfer posted this 02 May 2022

what i can add is, that this works also without an air-gap. but then you will need POC-coils for the 'magic' to happen. like wistiti did in his thread.

regards!

  • Liked by
  • Jagau
  • Augenblick
SonOfLuck posted this 07 June 2022

I just want to leave this(the original thread's pdf version) here:
Melnichenko's Effect 

Chris posted this 07 June 2022

Thanks SonOfLuck!

I still don't know what happened to this thread, however, whatever happened, it is now able to be rebuilt and read from scratch thanks to SonOfLucks PDF!

What a great team we have!

I have the thread in Backup, but I cant restore without loosing other information.

Best Wishes,

   Chris

Chris posted this 08 June 2022

Thanks to a few Members / Readers manual Backups, I have been able to restore this thread from those manual Backups without making any major changes to the database and loosing other Posts and threads!

I am still working on Images and Post specifics, so this is still a work in progress!

I bet Jagau will be happy as many other readers will also!

Thank You All, this is great to see!

Best Wishes,

   Chris

P.S: Please feel free to edit your own posts if you see it needs attention!

Chris posted this 09 June 2022

My Friends,

СВОБОДНАЯ ГЕНЕРАЦИЯ Андрей Мельниченко translates to: FREE GENERATION Andrey Melnichenko

Andrey Melnichenko's YouTube Channel is: www.youtube.com / channel/UCEtqI2EhN32Mvq7Wp5G9Vpg/videos

 

If you want to Create Your Own Thread and share your experiments on this topic, please feel free.

What is shown here, it is a very small part of a MUCH BIGGER Picture!

Best Wishes,

   Chris

Chris posted this 12 June 2022

My Friends,

After all the work restoring this Thread after it suffered a catastrophic error, and its now stalled and stopped?

That's a bit disappointing!

Best Wishes,

   Chris

Chris posted this 14 June 2022

@Jagau,

For an input of 4.5 watts I get 7 watts at output, this is the best performance so far that I have managed to get since I built devices like this.
1.56 is an excellent result to date.

So I confirm that melnicehnko's device is really abovetunity machine.

 

I wonder if you would like to publicly discuss the point of Magnetic Resonance, or where each Coil hits its Peak Voltage, for the minimum Input Power? This point is tuned for, both Frequency and Duty Cycle, to obtain maximum Output Power for the least Input Power.

Best Wishes,

   Chris

  • Liked by
  • Augenblick
  • Jagau
Jagau posted this 14 June 2022

Hello Chris

The first success in accomplishing the Melnichenko effect starts with understanding the first part.
The last schematic  published here is a simple modified flyback,

this first part must be realized and understood before going further in the project.
I am waiting to see replications before going further and continuing to explain.

It's not even a great effort required to do by the members here.


Jagau

Chris posted this 14 June 2022

Hey Jagau,

I agree with this:

The first success in accomplishing the Melnichenko effect starts with understanding the first part.
The last schematic  published here is a simple modified flyback, this first part must be realized and understood before going further in the project.

It is simple, again here is Jagau's Circuit:

@Jagau, I believe there is an error in this Circuit, please confirm.

 

Pretty much, this is a Bedini SG Circuit, and everyone is no doubt familiar with this Circuit! Its very Easy to Build!

Those Members searching for Answers, that have not already found Answers, and many have already and not Publically acknowledged it, please join in and Create your own Replication Thread: <Member>'s Melnichenko's Effect 

Best Wishes,

   Chris

  • Liked by
  • Augenblick
  • Mimo
Jagau posted this 14 June 2022

When the circuit was copied on the site it was too pale and conductors are missing this one is the good one

 

 
The second ground was barely visible. 

you'll notice there are two grounds in this circuit, so one doesn't affect the other, it's a modified flyback.

Jagau

Jagau posted this 20 June 2022

I've been very busy these last few days, I couldn't wait to go back to my experiences.

So I made myself a little gift, sometimes you have to have a little fun according to your budget, with a very special purchase, a TEK P5021 current probe. It's not the latest model but it works very well with my scope.

So still great experiences made and shared.


Jagau

Chris posted this 26 June 2022

Jagau is correct,

When Jagau says:

The crowd is not huge but many watch without speaking, as usual.

 

We get in the order of 10K Reads on this site a day, sometimes much more! Yet there is only about 1% joining in!

1% Trolls or ex-members that have wronged this site in one way or another! Because they have nothing to share of their own! Trolls trying to stop us because they are terrified of us!

So, Ronee, I appreciate you joining in and Sharing, I also wish to Thank You for doing so!

Learning about Asymmetrical Electromagnetic Induction is a very important step forward for Humanity!

Best Wishes,

   Chris

Chris posted this 02 July 2022

Hey Jagau,

Can you add any more information to my last post? More the merrier I guess.

For others watching and reading, we have done experiments where we can see a very large amount of Power Coming back to the Input:

 

This is on the Input Measurement Block: -1.63 Kilowatts!  Of Negative Power, not Positive Power, Power in the Spike going back to the Power Supply!

 

 

For the moment, I am not going to show where this is from, or discuss it further, as I already know what's possible, and seen this sort of thing for a very long time! I share this, because it will be of assistance to other researchers!

Other forums just do not ever discuss such things, because they cant understand it!

Best Wishes,

   Chris

Jagau posted this 02 July 2022

Hi all
It is always easier to understand how a system works by comparing it to examples of other known systems. In the case of the Melnichenko effect, I do not claim to have full mastery of the system but I will explain how I understand it.
Like many other functional existing systems everything is based on the big question:
How to circumvent the famous law of Lenz?
Whether it's the Adams engine or the latest Holcomb System, circumventing Lenz's law results in overunity. Electric iron or a high permeability material allows these systems to achieve this goal.


Quote from Dr. Robert Adams, the inventor of the well-known motor/generator:


One would expect the magnetic polarity reversal to be instantaneous in a rotating machine between the rotor magnet and the stator. However, this is not the case. I recently discovered that the inversion is exponential in the transition from one polarity to the other. When this happens, the magnetic radiation from the rotor pole(s) doubles without an external power supply. As a result of this attempt, I had meanwhile made an important discovery regarding magnetic polarity reversal, in that it was not necessary for the machine to be in motion or to apply external energy for it causes the reversal of magnetic polarity.

 

In the Adams generator, the rotating edge of the magnets and a synchronization at a very precise geometric angle produces this effect, in the Melnichenko effect the pulsed magnetic field of the coil L1 and with the rapid passage from one polarity to another produces a doubling of the magnetic radiation on the magnetic core of L2. As L2 is around this core it produces a doubling of magnetic radiation, as Dr. Adams said.

When degaussing L1 and modifying the flyback as in the drawing, this produces a BEMF at the closure of the pulse on the IGBT which is almost fully recovered in lamp no 1 minus the losses, that is why the consumption of the power source does not change.
 

In L2 when the current phases are well adjusted, this is the most difficult part, the L2 lamps light free without constraint of Lenz's law. Remember that the polarization by a magnetic field of a magnetic core has no resistance, is free and produces a doubling of radiation because the magnetic field of L1 is always there and has no constraint on L2 and as said if well Andrey is in no way magnetically bound to L1.

Quote from Andrey Melnichenko:
For the generation, a weak mutual polarization of the ferromagnetic cores through the gaps is also used in addition to the magnetic field of the magnetizing coil. In the axial position, it is optimal to insert two relatively long cores into the coil with their ends and bring out the main magnetic vortices from the ferromagnet,
when the induction of the magnetic field drops to zero or results in a partial reversal of the polarity of the magnetic field if the power source has a small current pulse polarity reversal or is supplied with alternating current with a component of constant current. Reversing the polarity of the magnetic field greatly reduces the transient process and the current decay time. This gives both a sharper induction decay front and an increase in EMF in the winding on a ferromagnet, which reduces source cost.

 

Do you remember this?

This is how I understand the Melnichenko effect.

 

P.S.

I forgot to tell you with the A.U members calculator you have what number of turns your L2 will have for maximum efficiency

that you coould find here:

https://www.aboveunity.com/thread/proof-of-coil-interactions-following-antenna-theory/


Jagau

Chris posted this 02 July 2022

Hey Jagau and all Readers,

Another excellent Post Jagau! Thank You!

Your statement:

How to circumvent the famous law of Lenz?

 

It is exactly correct and a very important fact for any Serious Researcher to Focus on! I mean, this IS the Ultimate Goal!

If I may, I see an avenue where confusion could set in for other Readers, so if you wouldn't mind me making a small point here?

First, I want to point out a passage from Floyd Sweet:

If the directions of the two signals are such that opposite H-fields cancel and E-fields add, an apparently steady E-field will be created. The energy density of the fields remain as calculated above, but the value of the E-field will double from E/2 to E.

 

I think its important to address what it is we are talking about when we see any Value of something double, or more, in Amplitude.

Of course, we are looking for a total Gain in Electric Power, over and Above, the Input Power. Therefore the arrangement we are focusing our attention on, must allow for a "Generational" aspect greater than the Input Power is essentially capable of by its self.

My opinion is, as the saying goes, a Picture is worth a thousand words:

Ref: Andrey Melnichenko - Transgeneratsiya electromagnetic field energy

 

If one is to evaluate the Vector Directions of each Field Individually, then one will see that a Superposition does occur, meaning there are some Vectors that Sum to Zero, for example: 1 + -1 = 0

Of course, the Vector Equation: 1 + -1 = 0 is Conventional Electromagnetic Induction, a frivolous approach to an almost 200 year old technology on Science's part!

There is more!

Asymmetrical Electromagnetic Induction is seen right there! This Vector Equation becomes: 1 + -1 + 1 = 1, of seen in Melnichenko's form: H1 + H2 + H3 = H3.

The Magnetic Field does not change Polarity, as in this case, a DC Source is the Supply, the Magnetic Field only changes in Amplitude, of Intensity, as the Magnetic Field Grows and Decays. So there is no AC, or Alternating Current seen, per se, its a DC Current Source for the most part, but the Primary Voltage Polarity flips between Mosfet TOn and TOff. So there is confusion seen amongst Researchers that have not yet put the work in!

Best Wishes,

   Chris

 

Edit:

P.S.

I forgot to tell you with the A.U members calculator you have what number of turns your L2 will have for maximum efficiency

that you coould find here:

https://www.aboveunity.com/thread/proof-of-coil-interactions-following-antenna-theory/

 

Hey Jagau, that thread is not currently Tier I, so some members will not be able to see it.

Do you think we could discuss allowing it to become public domain? I want to be sure we are ready to share more with the general public.

Jagau posted this 02 July 2022

I made correction for member calculator

accessible for all

https://www.aboveunity.com/thread/aboveunity-com-member-calculator/

jagau

Chris posted this 07 July 2022

My Friends,

Ironically, OverUnityResearch.com Member Itsu, several weeks after turning down an Invite, is now doing a replication of Jagau's work, Here!

My present replication of this basic circuit looks like this:





With this as diagram:




Some data on the used circuit:

L1 primary air core 80 turns: 726uH
L2 secondary 2x 144 turns ferrite cores separated by 1.5mm gap: 4mH    (this L2 is not yet in use in the present basic circuit!!).

When inserting L2 into L1 in the next step, the L1 inductance raises to 850uH.
When shorting this inserted L2, the L1 induction drops to 710uH.
But again, this L2 is now not in use!

FG running 1.4KHz @ 9% duty cycle (adjust to get ~120V across Lamp1)
Lamp1 120V / 4W

Initial power measurements shows for:

input power:   4.57W, see screenshot 1    (yellow: voltage, blue: current through csr and red calculated power)
IGBT power:   4.63W, see screenshot 2    (yellow: voltage, green: current and red calculated power)
Lamp1 power: 4.66W, see screenshot 3    (yellow / blue voltage (differential) , green: current through lamp1 and red calculated power)







As can be seen in the screenshots, the measured signals get more and more erratic and accurate power measurements gets harder to make.
I had to use the differential probing technique and advanced math function to measure the Lamp1 power due to its floating state.

It also shows that in this basic setup, almost all input power is being consumed by the Lamp1

Next step i guess would be to insert L2 into L1 and attach a load to L2 to see if this load (lamp2) can be lit for free (so without any
influence on the input power and Lamp1 power.

Side note 1: AboveUnity.com is often offline for some periods, so you might get some time outs.
Side note 2: the input DDM's (and PS meters) show lightly less current (thus power when calculated) as compared to the scope probaly due to the current AC component
in the signal.


Regards Itsu

 

NOTE: In the above image, you can see Itsu does have a Negative Power Component, pointed out in our thread: The Input Coil, which is Positive Voltage x Negative Current = Negative Power!

A Major Error seen, is the use of RMS Power Values! You can NOT use RMS Power Values on the DC Input Power, see our: Measurement Thread for an explanation!

Schooling the Gurus again, we are!

I have said it before, Itsu is a good Builder! He does good work! If Itsu was able to see through his projects and gain a greater understanding, he could be very successful!

I wish Itsu Luck, I truly hope he is able to see this Experiment through to the Knowledge required, However, I see a very important issue, that we here at AboveUnity.com have warned about before, do you see them? Digital Multimeter's? Yes? Don't use them! They are not accurate!

Also an Interesting observation:

AboveUnity.com is often offline for some periods

 

Yes, I have covered this, many times, its the Infrastructure I have had to put in to get up and running. We have limited Services, and also many cyber attacks against us, trying to take us down! 

Best Wishes,

   Chris

Chris posted this 10 July 2022

My Friends,

I believe we see more strife:

Doing some more accurate measurements on this new setup which includes L2 and its load see above post #2

Ref: Itsu's A Melnichenko effect replication

 

Now, I am sorry, but Itsu is no where near the mark! There is problem after problem after problem seen here!

Itsu states:

Input power:   4.71W  see screenshot 1

 

and we see:

 

 

Still Itsu is using RMS Voltage and Current Measurements, this is wrong and can not be used! This is NOT how you measure DC Input! This is In-accurate! Very Wrong!

 

Itsu's wave forms:

 

Itsu's waveforms are not inline with ours! I have no idea what itsu is doing! I mean, this is VERY Important to get right!

Of course, a bit of the Sawtooth waveform is seen clearly in Jagau's Screenshot, all three traces, it's not present at all in Itsu's!

Jagau showed early on:

 

 

Totally different Waveform, Totally different Effects! Totally Outside of the guidelines Jagau has set out... And Itsu is showing final measurements saying:

So this present setup with L2 does not show any special effect, but there are several tuning options which can be explored.

 

Sorry Itsu, your Work shows nothing special, this is certain!!! Your work, however, is NOT what Jagau has been showing everyone, you're comparing Apples and Oranges!

I am sorry, but the terrible attention to detail, when making a representation to our work, really does frustrate me beyond belief!

Itsu has not accurately replicated what we are showing!

Hmmmm, Accurate? No, not at all !!!

Best Wishes,

   Chris

Jagau posted this 11 July 2022

In most of our experiments taking measurements is the most important and at the same time the most difficult thing to do, especially since we use different waveforms. Don't get confused with pure DC and sine wave voltage, the way of calculating them is very different and moreover in my case at the input I have to take into account the duty cycle of the pulse

The voltage efficiency (average voltage) applies to a battery or DC voltage which is constant and does not vary over time,

this is what I am using in this Melnichenko experiment at input.


At the input we only have DC max volt or max amplitude pulsed. At the output we calculate it in RMS because we have a rectified sinusoidal output

and as you know RMS is the DC equivalent used for a sinusoidal curve wich varies over time.

Below you will find valuable help on which formula to use and in which case of the waveform,

The one that is of our interest is the PULSE WAVE

 

Jagau

Chris posted this 11 July 2022

My Friends,

Jagau is Correct, and, Schooling the Guru's Again! Thank You Jagau!

A MUCH better result from Itsu:

Ref: Itsu's A Melnichenko effect replication

 

I would strongly recommend increasing the size of the inner core, by at least three times, and use a much bigger gauge wire to reduce the Coils Impedance. This will allow a greater Power Output on this Coil.

Jagau may want to share more on the optimum output gain for the Secondary Coil? We have a method of calculating the optimum Coil Length / Inductance.

For Itsu:

Continuing the search.......

For Chris:   

?t=312

 

Your Input is NOT AC Itsu!

RMS is Not Correct for DC Measurements on the Input! Sorry the Video you shared does very clearly show that RMS is ONLY Accurate for AC Sinusoidal Source Waveforms! I urge you to do some very simple Math that can very easily prove this simple fact. Please see our: Measurements Thread!

It is NOT correct to use RMS on a DC Source, period. Sorry, but this basic fact must be realised by any Serious Researcher. A Non-Linear Load can also prove this fact, and give the greatest margin of Error from a DC Source. I would put this to Verpies, he is the only one over there that can verify this simple fact. 😉The others just don't have the expertise! See Here for a little extra information.

A DC Source designed for Conventional Current:

Conventional current flows from the positive pole (terminal) to the negative pole. Electrons flow from negative to positive. In a direct current (DC) circuit, current flows in one direction only, and one pole is always negative and the other pole is always positive.

 

Is physically unable to supply Negative Currents, and in this Case, RMS is all inclusive of Negative Currents, adding them to the Input:

 

Including the Red part of the above Image as Input Power, when it is NOT! Its Negative Power!

 

Power Flow in a Four Quadrant Argand Diagram

 

RMS Math:

 

Instantaneous Readings:

  • 1 Volt x -1 Amp = -1 Watt
  • √((1 Volt x -1 Amp)2 / 1) = 1 Watt = INCORRECT !!!

 

Again, please do the Math, this will prove it to you and show the voices that are in your ear, to be completely WRONG AGAIN !!!

Of course, a DC Power Source is Incapable of Supplying Negative Conventional Current when it is designed to Supply a Positive Conventional Current!

 

EG:

  • 1.28 Watts RMS
  • 0.0957 Watt's Average

 

Isn't it? Well? Honestly... Does anyone not see a problem with the guru's stupidity? Can a DC Source Supply the Reverse Current? No! Its then an AC Source isn't it !!!

Please Itsu, do your own Homework, careful who you listen to!

Schooling the Gurus again, we are!

 

Load Impedance is important, we have said this for quite some time now, and yet LED's are not the best load. Don't use CFL's:

LED bulbs refer to artificial lighting devices that use tiny solid-state semiconductors to produce light. On the other hand, CFL bulbs connote the lighting device that uses electrical discharge to induce the gases present in the tube, that releases UV light, that affects the phosphor to produce bright visible light.

 

I am pleased to see Itsu's effort, and the humble approach now adopted, Thank You Itsu!!!

Best Wishes,

   Chris

P.S: I see some Trolls joining the party over there... Maybe they might learn something, one never knows with Trolls!

Some of the dumbest things are said by the dumbest people sometimes! 🤡Shame!

Jagau posted this 12 July 2022

 

Hi all

As for the dimensions of the core, I refer you to line 009 of the attached document.

There is no ready-made formula, it is through experimentation that we find.

You have to work a little to succeed and it's those who work who succeed, not those who only copy.

 

A few years ago Adrian S. Nastase Phd Electronic engeenering said:You can think of it like this: 

You can think of it like this: A pulse signal with its amplitude between 0 and Vp (its peak value)and a duty-cycle d, has the average value:
VpulseAverage = d*Vp

Jagau

Attached Files

Chris posted this 12 July 2022

My Friends,

I am sad to report, the response from Itsu is not a sensible, logical approach:

For Chris,

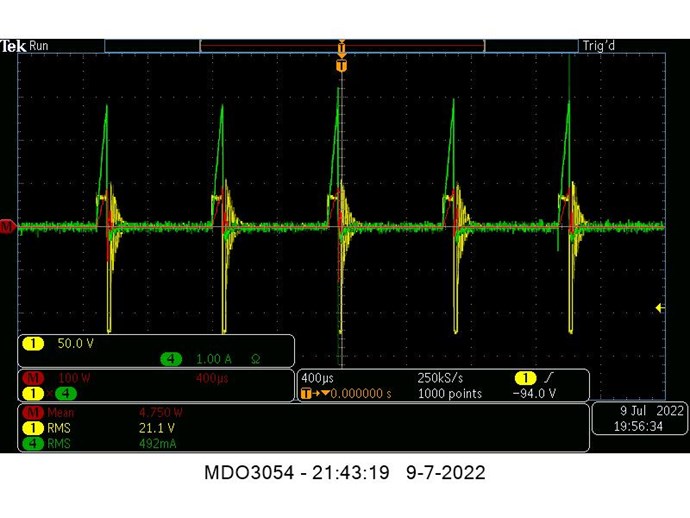
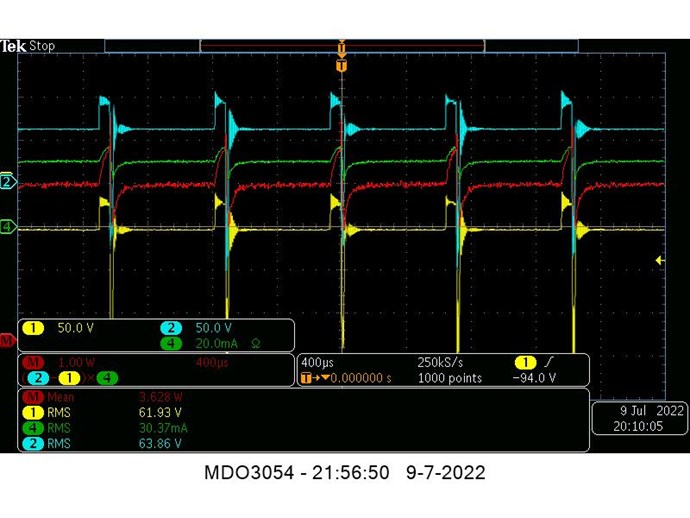
the beauty of power measurements with a scope is that the scope does not care what kind of signal it has, DC, AC, peak, square, sinuous etc.
It just takes millions  of samples of the signals (not rms, not mean, not ...) from its buffer and multiply (in this case) those instantaneously getting millions instantaneous power values which then get averaged (mean) presenting the average power across that buffer.

So nobody is using rms value's to calculate power, those rms value's you see on the voltage and current are JUST a representation of the signals measured by the scope, it does NOT use them for calculating power.

I don't pretend to be a guru in anything, so please anyone with extended knowledge on scope power measurement techniques step forward and either confirm, deny and/or improve on my above statement.


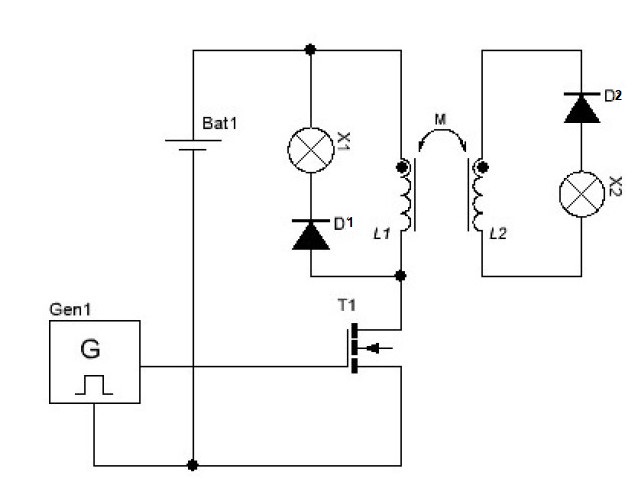
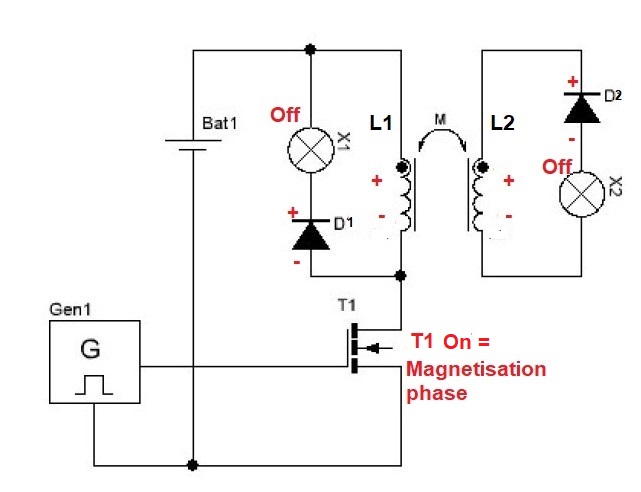
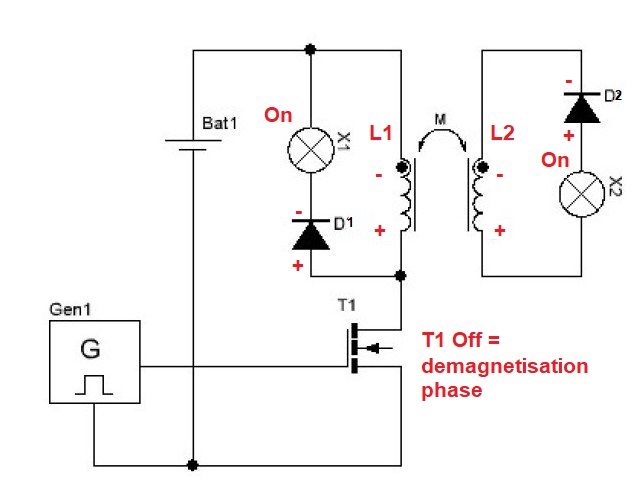
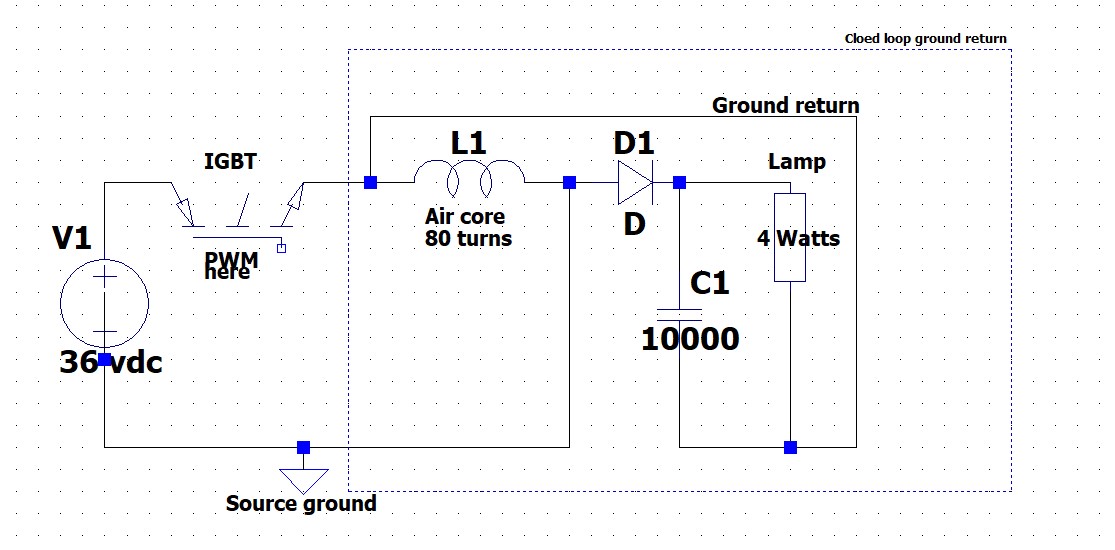
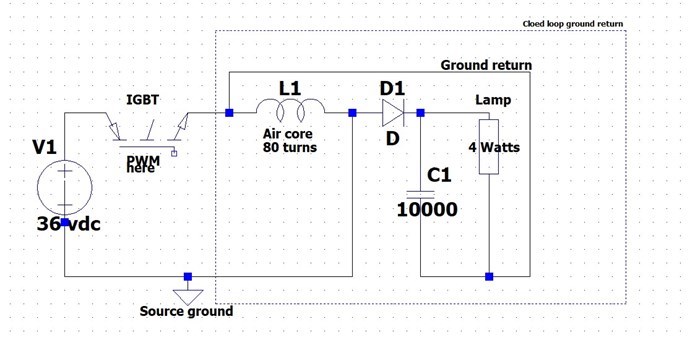
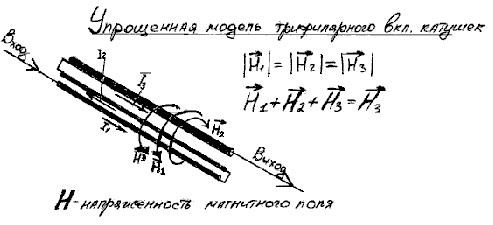
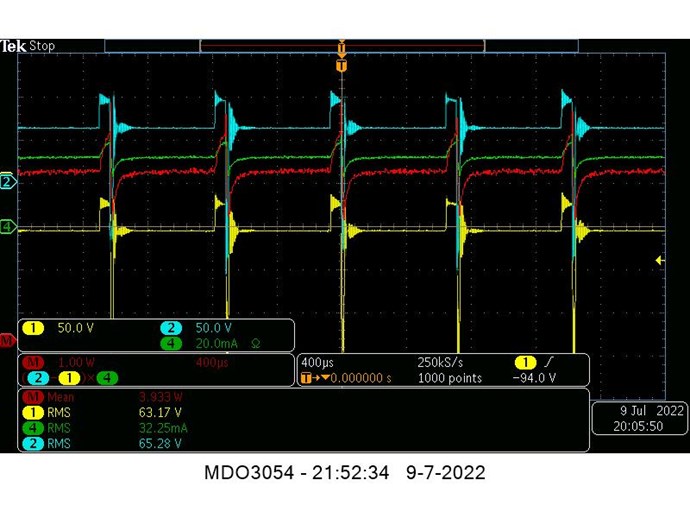
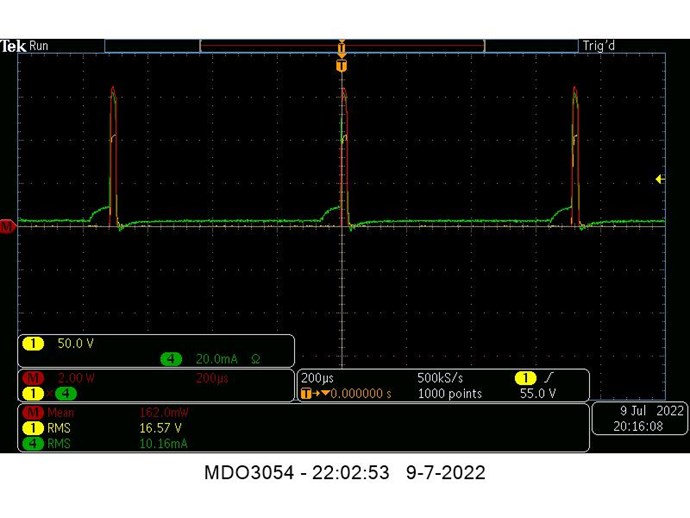
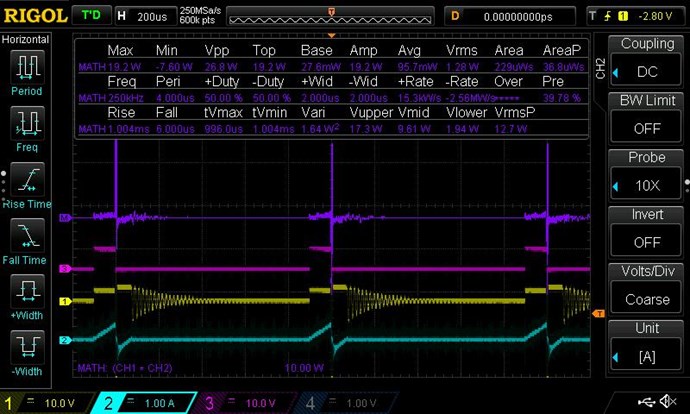
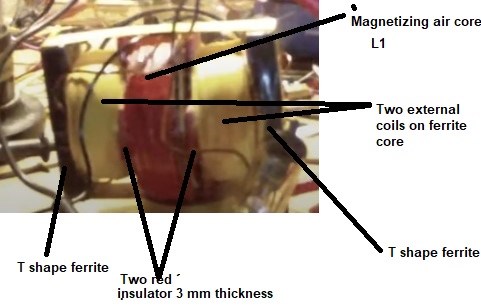
Concerning the dimensions of L2, i did use several different L2's, see above post #7, but all shows similar output value's (65 to 160mW), so i hope Jagau can shed some light on what dimensions he uses to get cop > 1.

Regards Itsu
   
Itsu

Ref: A Melnichenko effect replication

 

I understand what you are saying Itsu, I understand very well how a Scope works, Thank You.

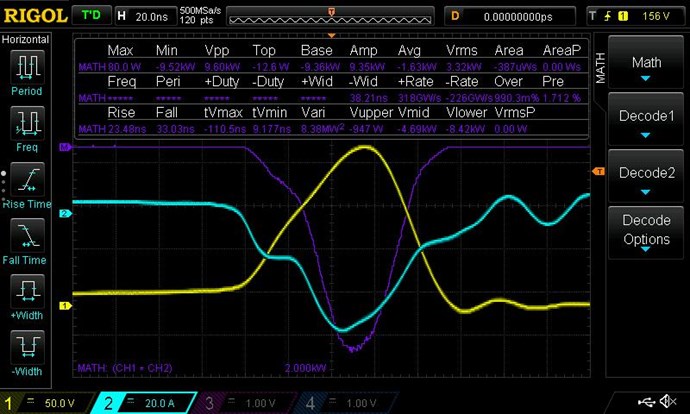
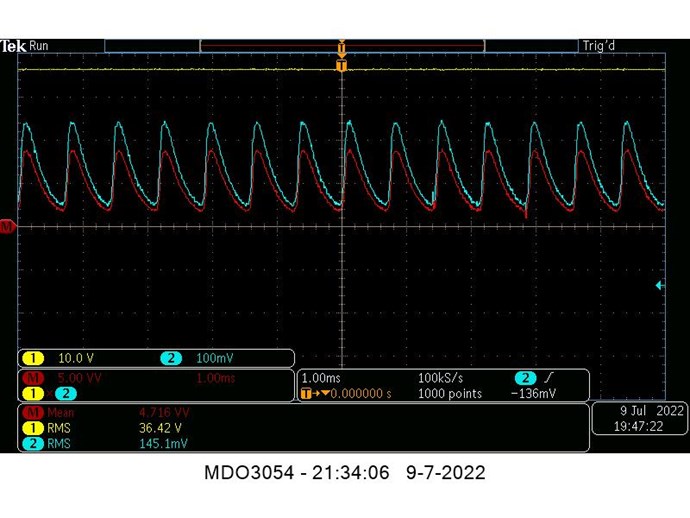
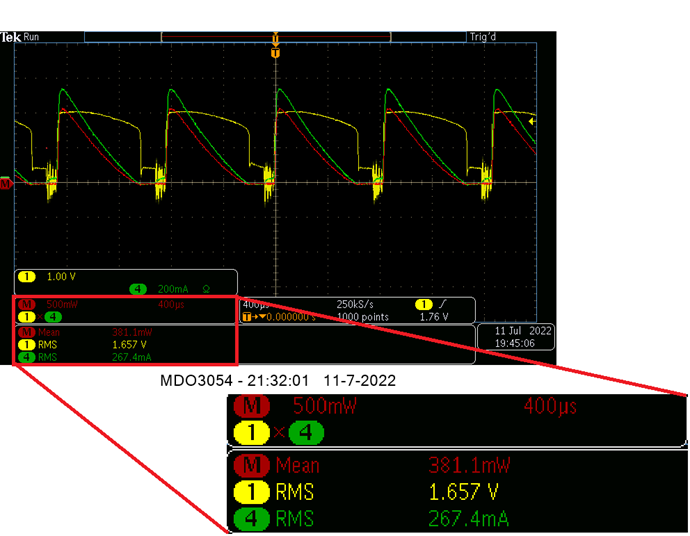
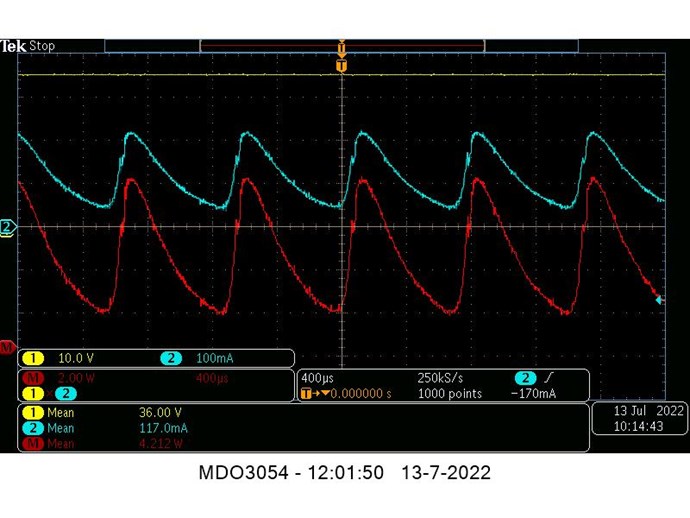
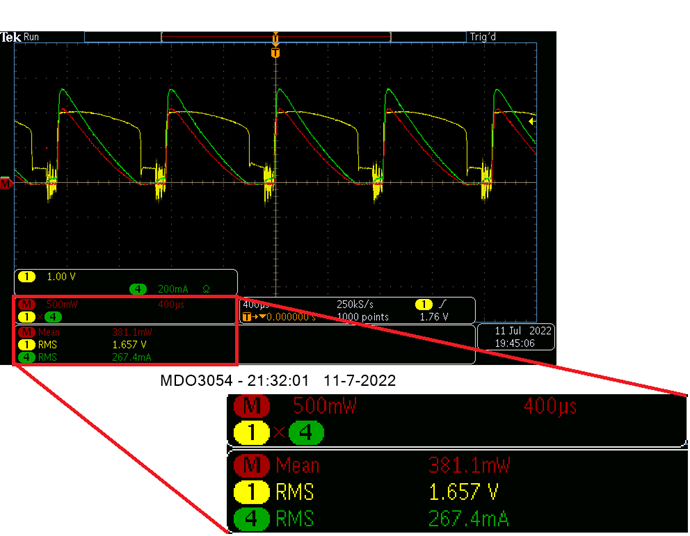
Your Scope is taking the RMS Values for that Channel:

 

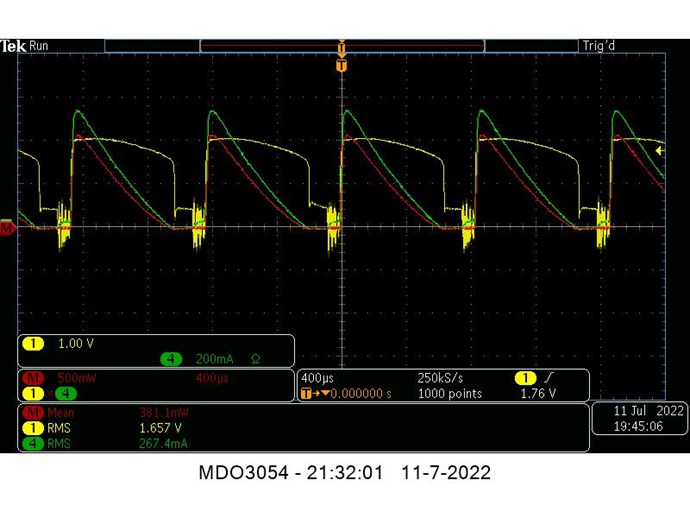
You are averaging: Instantaneous V RMS x I RMS = P in Watts

  1. 1.657 V RMS
  2. 267.4 mA RMS

 

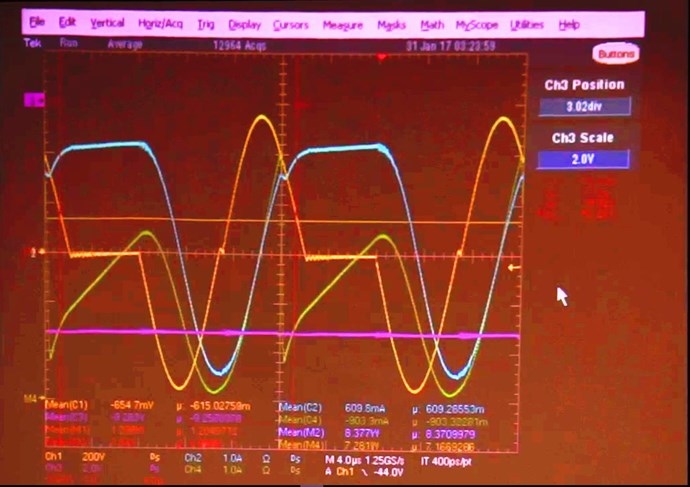
Which is Wrong! You cant do it this way, not on DC Input! I know this scope shot is not your Input... But using this as an example.

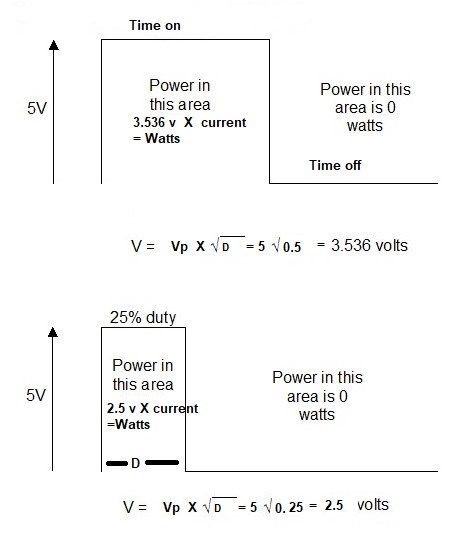
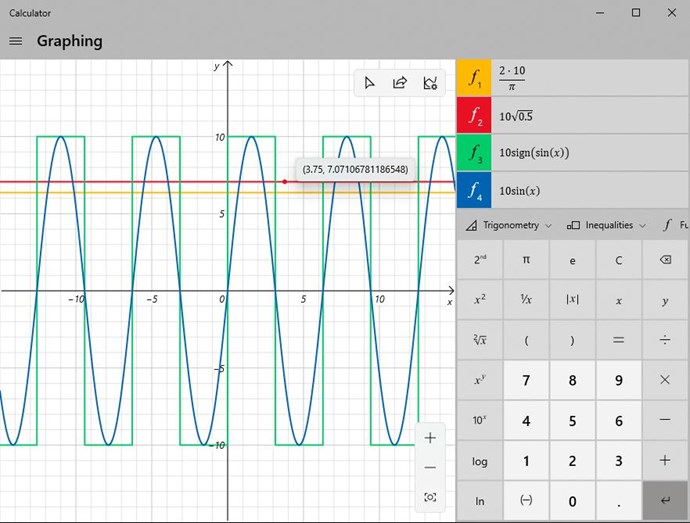
Very simply, compare a Sinusoidal Waveform with each channel, one Mean and one RMS, the difference will amaze you! I have already shown this in the: Measurements Thread, if you go and Read it!

However, any setting on RMS means you have the Scope Calculating RMS for the Buffer Size across the data points captured. 

 

RMS is Specifically designed for AC, Alternating Current Only! It can NOT be used for DC, Direct Current, at all.

RMS or root mean square current/voltage of the alternating current/voltage represents the d.c. current/voltage that dissipates the same amount of power as the average power dissipated by the alternating current/voltage. For sinusoidal oscillations, the RMS value equals peak value divided by the square root of 2.

 

Ref: RMS Current

 

The Oscilloscope will take the RMS Value, if you capture the RMS Value, again, which is wrong! Please do the Math!

The term “RMS” stands for “Root-Mean-Squared”. Most books define this as the “amount of AC power that produces the same heating effect as an equivalent DC power”, or something similar along these lines, but an RMS value is more than just that.

Ref: RMS Voltage Tutorial

 

Its a real shame, because not a single measurement can be accurately represented, unless the Correct Data Points are Calculated! Its sadly a fact, that these are the same people, telling Itsu how to measure incorrectly, that have been telling everyone for decades, that their Measurement Data is wrong! I can show you thread after thread that states that you should use RMS on a DC Source, when you absolutely Should NOT !!!

Ask yourself, why have they insisted on RMS for so long? Is it a means to falsify the Data just in case others did get something of Value? 

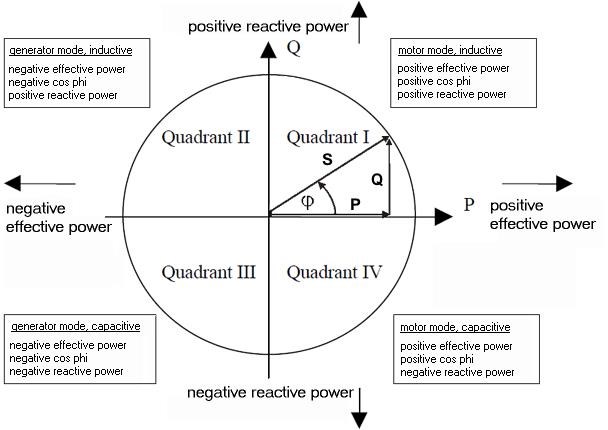
RMS can NEVER Measure any Negative Power, RMS is ALWAYS Positive, never accounting for any Reverse Currents! It Should NOT be used on DC if one wants Accurate Measurements! Should we not expect measurements to be accurate if measurements are to be given?

For those providing Measurements, they should be providing accurate Measurements, that are in-line, with Industry Standard Definitions, and Defined Values and Guidelines!

I have provided the evidence, the proof is right here, with References, if you persist to make in-accurate measurements, I can no longer assist.

This is Jagau's Thread and I do not wish to waste any more resources on his Thread, Sorry Jagau!

Best Wishes,

   Chris

SonOfLuck posted this 13 July 2022

( Hi Chris

(I'm pretty sure I will be labeled a troll for this, which i'm not)

You are averaging: Instantaneous V RMS x I RMS = P in Watts

  1. 1.657 V RMS
  2. 267.4 mA RMS

1.657 * 0.267 = 0.442419 ~= 442mW
This is not the value that Itsu reported for this image.
Itsu stated 381 mW wich is the mean of ( V measures multiplied by A measures )

itsu measurment

And you saying that's the correct way. Every wattage reported by Itsu was calculated this way, you can check.
Sorry Jagau! )

  • Liked by
  • Chris
  • Augenblick
Chris posted this 13 July 2022

Hi SonOfLuck,

Yes, I have done the math, which is not a conclusive answer to the problem!

If Itsu can show in Scope Math Functions where he is setting Mean or Average Values for each Channel, I will accept his answer, however, currently, the Scope is showing RMS Values! Of course I have already pointed this out.

 

EDIT:

 

Post 1:

 

Post 12:

 

There you have it, Margin of Error: ≅ 0.5 Watts, a large error! 10.43%

Even with less cycles on the screen...

If a Scope Shot is shown, then the Scope Shot should show the Correct Values! Other wise its misleading and incorrect, Accurate Measurements can NOT be assumed, again as is pointed out.

Mean or Average, same thing, must be used on DC Input!

Best Wishes,

   Chris

  • Liked by
  • Augenblick
Chris posted this 13 July 2022

Thank You Itsu:

 

 

Thank You for showing Correct and much more Accurate Measurements. More coming soon, stay tuned...

FYI, Brian's Thread has some more data.

Best Wishes,

   Chris

  • Liked by
  • Jagau
  • Augenblick
Jagau posted this 13 July 2022

Taking measurements in our ongoing experiments is as important as the experiment itself.


I have no objection to everyone contributing in the way of taking measures that will have a certain value. However, we must do it with a certain order and respect for others because we are all here to learn and we do not all have the same skill to experience.

That being said I congratulate here on this forum and all those who experiment on the Melnichenko effect as well as Itsu who is a member of another forum and who also makes great efforts to achieve this experiment. If other forums want to experiment and well by my humble little thread on the Melnichenko effect, I will be delighted and the whole community of researchers will make sure that we succeed together.

It seems misunderstood that when we are in the presence of different waveforms the way of calculation is different , in our case here i will explain how take measurements in the presence of a pulsed voltage from 0 to Vmax.

It will be the subject of the following post


Jagau

Chris posted this 13 July 2022

Hey Jagau,

You're a noble, honorable, and very skilled Member! Thank You for all your Efforts! Its a pleasure to have you here with us!

It is a shame, that none of the so called experts, came to Itsu's aid! - What happened there?

FYI: 2015 Do NOT use RMS:

which generates an instantaneous power waveform, then take the _average_  (not RMS) value of that IP waveform.

Ref: Accurate Measurements on pulsed system's harder than you think.

Interesting read, observe Names and Recommendations for more insight!

 

I am sure the non-public thread over at the other forum is filled with panic and desperation right about now... What are they Cooking up now I wonder?

Best Wishes,

   Chris

Chris posted this 14 July 2022

My Friends,

Jagau has given us an Equation that Calculates the Average Voltage:

You can think of it like this: A pulse signal with its amplitude between 0 and Vp (its peak value)and a duty-cycle d, has the average value:
VpulseAverage = d*Vp

 

Lets look at some examples:

  • Voltage Peak VP = 10 Volts
  • Duty Cycle d = 50%
  • VAverage = d * VP = 0.5 * 10 = 5.0 Volts Average

 

Another:

  • Voltage Peak VP = 10 Volts
  • Duty Cycle d = 10%
  • VAverage = d * VP = 0.1 * 10 = 1.0 Volts Average

 

These Average Values, they are logical! They Make sense for an Average Value.

Thank You Jagau!

Best Wishes,

   Chris

Jagau posted this 14 July 2022

Hi Chris
Maybe an example with an image is easier to understand.

It is very very important that this applies that in the case of a square wave which does not go down below 0 volts, it is always positive. If you have a square wave varying from plus to minus you should not use this formula.

 
 

Jagau

Chris posted this 15 July 2022

Hey Jagau,

With your Statement:

It is very very important that this applies that in the case of a square wave which does not go down below 0 volts, it is always positive.

 

I completely agree with this statement!

I posted this image to Brian's thread, and think it is sensible to also post here:

 

 

I have a problem with the math, not with what you are saying, but with the Area Under the Curve. In other words, the Integrated Area in a Single Cycle.

 

We have Data Points that are recorded on the Scope, and all Area under the Waveform, above Zero is Active Area that is to be used in the Calculations of Power. Some well known Area Equations:

  • Square area formula: A = a²
  • Rectangle area formula: A = a * b
  • Triangle area formulas:
    • A = b * h / 2 or
    • A = 0.5 * a * b * sin( γ ) or
    • A = 0.25 * √( ( a + b + c ) * ( -a + b + c ) * ( a - b + c ) * ( a + b - c ) ) or
    • A = a² * sin( β ) * sin( γ ) / (2 * sin( β + γ ))
  • Circle area formula: A = πr²
  • Circle sector area formula: A = r² * angle / 2
  • Ellipse area formula: A = a * b * π
  • Trapezoid area formula: A = ( a + b ) * h / 2
  • Parallelogram area formulas:
    • A = a * h or
    • A = a * b * sin( angle ) or
    • A = e * f * sin( angle )
  • Rhombus area formulas:
    • A = a * h or
    • A = ( e * f ) / 2 or
    • A = s² * sin( angle )
  • Kite area formulas:
    • A = ( e * f ) / 2 or
    • A = a * b * sin( γ )
  • Pentagon area formula: A = a² * √( 25 + 10√5 ) / 4
  • Hexagon area formula: A = 3/2 * √3 * a²
  • Octagon area formula: A = 2 * ( 1 + √2 ) * a²
  • Annulus area formula: A = π( R² - r² )
  • Quadrilateral area formula: A = e * f * sin( angle )
  • Regular polygon area formula: A = n * a² * cot( π/n ) / 4

 

If we use: 10 VoltsPeak, and a Duty Cycle of: 50% and set our Area to 100 Squares, for One Cycle:

 

 

I have to say, I am not in agreeance with Dr Adrian S. Nastase. We get a result that does not appear to be correct:

  • RMS of 10 VoltsPeak = 7.07106781 Volts, or 70.7106781 Squares above the Zero Line in One Cycle.
  • Average of 10 VoltsPeak = 5.0 Volts, or 50 Squares above the Zero Line in One Cycle.

 

Taking One Cycle, at 10 Volts and 50% Duty Cycle, then we get:

  • 100 Squares x 0.5 = 50 Squares at 10 Volts, and 50 Squares at Zero Volts.

 

Over one Cycle, we have an Average Voltage of 5 Volts, so the Green line makes sense to use, as the RMS gives a greater usage of Voltage, by 2.07106781 Volts. Because the Sine Wave is Non Symmetrical between Zero and Peak, I fully understand why RMS is used for Sinusoidal Waveforms:

RMS means ‘Root Mean Square’ in mathematics. It is also referred to as quadratic mean. The RMS is very useful in many fields, particularly in electrical engineering and in the domain of signal amplifiers. RMS is very useful when the random variables in the data are negative and positive such as sinusoids.

Read more: Difference Between RMS and Average

 

I just cant make sense of this Jagau, sorry My Friend, but to me, this is not Correct?

For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load.

 

I just can not agree that RMS is valid for Square Waves, or on a DC Input Source. I am sorry My Friend... 😉

Which means less Input in the end.

   Chris

  • Liked by
  • Augenblick
SonOfLuck posted this 15 July 2022

Hi Chris,

Consider this....

1V peak pulse(0 bottom) with 50% duty cycle on a 1 ohm Resistor gives us 1A peak pulse.
if you multiply the measured data points you get 1 W peak pulse.
Now you average it and you get 0.5 W.

Now if you average the 1V pulse and 1A pulse, that gives us 0.5V and 0.5A, this value feels right ( to me at least) in the individual context, but if you multiply them that's 0.25W.

 

Now if you RMS the 1V pulse and 1A pulse, that gives us 0.707V and 0.707A. For me its weird to say that

1+0+1+0+1+0+1+0+......+1+0

a series like this the average value to be 0.707, BUT if you multiply the values that's 0.5W.

 

From this it's seems like RMS is king, but we don't need to go far to see that's not truly the case.
itsu measurment

Here the RMS V and A multiplication gives different W than the measured and averaged value, 381mW vs 442mW.

 

Best regards,
SonOfLuck

 

Chris posted this 15 July 2022

Hey SonOfLuck,

Some good points there! I am running an experiment at the moment. Long winded math to show the RMS and Mean are totally different Math Problems and that RMS should not be used on DC or even Pulsed DC Systems, in General.

If you look at the Pro's, Graham Gunderson, he uses Mean:

 

Graham Gunderson is a very high level Electronics Engineer in my opinion, he has worked in many High level positions and is a professional at what he does.

TinselKoala, TK has a very extensive history in Metrology and he uses Mean, recommends to NOT use RMS:

which generates an instantaneous power waveform, then take the _average_  (not RMS) value of that IP waveform.

Ref: Accurate Measurements on pulsed system's harder than you think.

Interesting read, observe Names and Recommendations for more insight!

 

I have to agree, when you say:

From this it's seems like RMS is king, but we don't need to go far to see that's not truly the case.
itsu measurment

Here the RMS V and A multiplication gives different W than the measured and averaged value, 381mW vs 442mW.

 

Its not hard to show mathematically, that RMS is not always Correct! However, like Jagau said:

It is very very important that this applies that in the case of a square wave which does not go down below 0 volts, it is always positive. If you have a square wave varying from plus to minus you should not use this formula.

 

Generally, RMS and Mean, in most Positive going V and I, the Values will be pretty similar. I showed this in my video here:

 

RMS is an AC, Alternating Current Calculation:

 

For DC and Pulsed DC Systems, generally Mean or Average Should be Used. This is especially true when one has a Non-Linear Load.

Best Wishes,

   Chris

Chris posted this 16 July 2022

My Friends,

Itsu's center coil:

 

 

does anyone see a problem with it?

 

Increasing CSA by packing the core with tape?

Best Wishes,

   Chris

  • Liked by
  • Augenblick
  • Jagau
Jagau posted this 17 July 2022

Hi Chris
Sorry for the long return, very busy with my family these days.
In the meantime, what we are doing here is very important, we will establish the basics of a simple but effective calculation for our projects like this. There is no forum on the planet that has actually done to date.
Let's be patient and take the time to find the solid and certain formula.
I will make other comments later to discuss this very interesting point.
jagau

Chris posted this 22 July 2022

@Jagau - Should we let the cat out of the bag?

 

@Itsu, work with this in mind:

  • Voltage is "Generated", via Charge Separation.
  • Current is Pumped. via M.M.F Opposition.

 

 

Making a few Coils do More Work in the System is very easy when one realizes that one can manipulate the Magnetic Field to do the Generation for you...

Best Wishes,

   Chris

Chris posted this 31 July 2022

@Itsu,

You need to study what CSA or Cross Sectional Area is! How it works and why its IMPORTANT!

You're wasting your time with this:

Ref: WTF Man?

I really don't know why some people persist with something that is not going to work!

 

If you happened to study Melnichenko, you would see, as I have already told you, the Core is about three times bigger:

 

СВОБОДНАЯ ГЕНЕРАЦИЯ Андрей Мельниченко translates to: FREE GENERATION Andrey Melnichenko

Andrey Melnichenko's YouTube Channel is: www.youtube.com / channel/UCEtqI2EhN32Mvq7Wp5G9Vpg/videos

Andrey Melnichenko's Core is about three times the size of Itsu's at minimum!

A Replication requires some Attention to Detail!

Best Wishes,

   Chris

Chris posted this 31 July 2022

My Friends,

See what I mean:

gyula has asked me to comment on Melnichenko's statements he posted in Reply#40 above.  The set up Itsu has just tested can be modeled in FEMM using the axisymmetric method which is a true 3D solution.  I have done this modeling the core with greater mu in the r dimension (the radial dimension) than the z dimension (the length dimension).  I used mu = 10,000 for the radial dimension and mu = 100 for the length dimension.  There is no overunity in that situation.  Melnichenko is correct in making observations that the anisotropy of the core will affect the magnetic energy stored for a given ampere turns of current, but I can find no evidence that this can lead to OU.  My opinion on his other statements of dividing the core into individual sections each with its own winding is that also will not produce OU.  I will have a go at doing a simulation of such an approach and report back.
Smudge 

Ref: A Melnichenko effect replication

 

Hey good idea, try to simulate this, "a true 3D solution" WOW... That will give you a definitive answer... For SURE 🤪

Just maybe, a simulation of something you have ZERO Idea about will give you some answers?

AH: I really don't think so!

Hmmm, well, it can and does, go Above Unity, when this is done correctly, but by all means, write this off before you even understand how Above Unity Machines Work! That's a good idea!

Smudge is completely Wrong, Entirely Wrong! When Smudge realises why The Generator Shaft has nothing to do with the Electrical Energy output on the Electric Generator, that Shaft Torque is a By Product of the Electrical Energy and not the Cause, then maybe he might have a bit more success...

Hmm, all I can do is shake my Head!

Best Wishes,

   Chris

Jagau posted this 01 August 2022

Hi friends
Back from a trip, I will take the time to read, a little late to resume.
Jagau

Jagau posted this 03 August 2022

When Melnichenko talks about three-core this is what he's talking about.

 

This image taken from a video of Melnichenko


The center air core or magnetization coil and the other two at the T-shaped ends, wth 3mm insulation in red

Jagau

Chris posted this 03 August 2022

My Friends,

I can confirm, Jagau's recommendation will, under specific conditions, work as is intended!

Don't forget however, Coil Geometry defines the Magnetic Field, the Magnetic Field defines Voltage "Generated" via Charge Separation, and the Current Pumped via Opposing M.M.F's! So, Design is an important factor here.

Best Wishes,

   Chris

Jagau posted this 03 August 2022

 

Hi Chris

In the arrangement of the air core on the magnetic core,

the coupling coefficient is a paradox, it works in reverse,
Statement from Melnichenko, at line 39 his patent 2022


 It is important to simultaneously increase the magnetization and, at the same time, weaken the magnetic coupling of the ferromagnet with the inductor

This is one of the most important things about his invention,

it shouldn't have almost any magnetic feedback effect on the primary,

but as he says in his videos there is always a little.

Jagau

Chris posted this 03 August 2022

Hey Jagau,

You are correct! The equation: H1+ H2 + H3 = H3 also shows this, also the equation I came up with: 1 + -1 + 1 = 1 also verifies this.

However, one must have a very good Magnetic Resonance! Slightly out of resonance and this is changed greatly!

Floyd Sweet was down in the Microwatts, I am still in the Milliwatts so still have some work to do yet. Magnetic Field H, or M.M.F. is a Factor, increase H or the M.M.F, and this helps!

 

@All Readers

Please Note, Jagau has succeeded simply because he has put in the work! Study and also experiment! Jagau has followed the path with an open mind, and investigated phenomena properly!

If you do the same, you will succeed also! We will help you all the way!

 

Best Wishes,

   Chris

Chris posted this 03 August 2022

Appologies to Jagau for posting Itsu's work here, please say and I will move to another thread if you wish?

I want to quote:

I did some measurements on this new BIGGER L2 coil made of 3 stacked ferrite toroids as core

Using a 100 Ohm 1% induction free resistor as lamp1 and a 12V / 5W lamp as lamp2, i have a 219 / 211V BEMF spike across L1 @ 36V input voltage.

FG:1.5KHz @ 10% duty cycle


The input power in that situation is:

with lamp2 load off:   3.2W
with lamp2 load on:   3.2W   


The power into the 100 Ohm lamp1 load is:

with lamp2 load off:   3.2W
with lamp2 load on:   2.1W   


The power into the lamp2 load is:

with lamp2 load off:    0mW
with lamp2 load on: 855mW     some light in the 12V / 5W lamp


At 36V input voltage, the lamp2 load when switched on does take / shares its power from Lamp1 once again.

Efficiency with:

Lamp2 load off:  3.2W /  3.2W = 1      = 100%            Max. efficiency up till now with L2 off
Lamp2 load on:  2.95W / 3.2W = 0.92 = 92%         


Itsu

 

@Jagau, any Recommendations for Itsu?

 

I have many, but will wait for others to share their opinions first!

Best Wishes,

   Chris

Jagau posted this 03 August 2022

Hi Chris

Itsu's works are going very well here, he makes a lot of effort to get a good result and I respect his ideas, he does various tests and several kinds of experiments like the last one with a linear load at the nput.

This is how we advance by experimenting.
The most important recommendation is taking measurements, input versus output.

I'm pretty sure many have tried the Melnichenko effect but don't understand how to take and interpret their measurements and they may have been successful without knowing it.

I confess that I would like to see as many efforts of the members here. Many read here and don't share anything.
Jagau

Chris posted this 03 August 2022

Hi Jagau,

I agree 100% with your statements!

Any Recommendations for Itsu?

Best Wishes,

   Chris

Jagau posted this 03 August 2022

Yes  I made them in the last post with the 3 photos,

don't worry he will understand,

he still likes to read here like many.

Jagau

Chris posted this 04 August 2022

My Friends,

Jagau is correct, some Coils work better than others! Largely this is due to the Coils Geometry!

However, If I may,

I would suggest Itsu stay with his current coils only checking the VOut individually on each Coil at TOFF on the Mosfet. Comparing VOut in a Single Scope Shot. Making sure the Scope Triggering is set to L1 only so we can see the Timing.

Then I would like to see a scope shot of L1 and L2's Currents, making sure the Phase is correct and the method defined, e.g: Conventional Current or Electron Current. Of course, this is to inspect the function of L1 and L2's Opposing Magnetic Fields, a Very Well Known Requirement as we all know!

Itsu needs to find the Resonant Frequency of the Coils individually, but in the current configuration! We need to know the range in which we are working in and compare to current frequencies!

Itsu last stated:

FG:1.5KHz @ 10% duty cycle

 

So, lets see where Resonance lays and compare. Don't forget, Reducing the Duty Cycle is like a Change in Frequency you could almost say. Coils behave according to Antenna Theory, so the fundamental Resonances are Important!

Region of Interest:

ROI ≅ L1 Resonance + L2 Resonance / 2.

 

Lastly, if Itsu can confirm the Turns on L2 vs L1, as L2 needs to be more turns, and we can go into this later on.

Some advice, stay on track! Look at the Effects First, then the Measurements! I expect you should have seen one or two anomalies on the scope about now! I guess if you're not looking?

Itsu, look for this:

 

 Your 10% should be the Regauge Period! Look for this and work on this, this is Asymmetrical Regauging and once done right, you will see a whole new world open up for you! Your Input will be Insignificant compared to the Output! You know you have something when you gain this operation! Which is really easy!

Best Wishes,

   Chris

P.S: All this has been covered here for many years now 😉

Topic Is Locked

We're Light Years Ahead!
Our Above Unity Machines:

Asymmetrical EMI

Wistiti's Bucking Joule Thief
Non-Inductive Coil Experiment
CD's Non-Inductive Coil Rep
Baerndorfer's Experiment
Captainloz's A-R-E
Aetherholic's COP>4.0

Resonant EMI

Yo's Ferro Resonance
Jagau's Non-linear Resonance
Ferrite at work
Recomended Protocol:
Measurement
Switching System
Measurement Block
Current Observation
Current Sensing Resolution
Members Online:
What is a Scalar:

In physics, scalars are physical quantities that are unaffected by changes to a vector space basis. Scalars are often accompanied by units of measurement, as in "10 cm". Examples of scalar quantities are mass, distance, charge, volume, time, speed, and the magnitude of physical vectors in general.

You need to forget the Non-Sense that some spout with out knowing the actual Definition of the word Scalar! Some people talk absolute Bull Sh*t!

The pressure P in the formula P = pgh, pgh is a scalar that tells you the amount of this squashing force per unit area in a fluid.

A Scalar, having both direction and magnitude, can be anything! The Magnetic Field, a Charge moving, yet some Numb Nuts think it means Magic Science!

Start Here:
Help with using the Forum.
Message from God:

Hello my children. This is Yahweh, the one true Lord. You have found creation's secret. Now share it peacefully with the world.

Ref: Message from God written inside the Human Genome

God be in my head, and in my thinking.

God be in my eyes, and in my looking.

God be in my mouth, and in my speaking.

Oh, God be in my heart, and in my understanding.

Your Support:

More than anything else, your contributions to this forum are most important! We are trying to actively get all visitors involved, but we do only have a few main contributors, which are very much appreciated! If you would like to see more pages with more detailed experiments and answers, perhaps a contribution of another type maybe possible:

PayPal De-Platformed me!

They REFUSE to tell me why!

We now use Wise!

Donate
Use E-Mail: Chris at aboveunity.com

The content I am sharing is not only unique, but is changing the world as we know it! Please Support Us!

Thank You So Much!

Browse by Category:
Weeks High Earners:
The great Nikola Tesla:

Ere many generations pass, our machinery will be driven by a power obtainable at any point of the universe. This idea is not novel. Men have been led to it long ago by instinct or reason. It has been expressed in many ways, and in many places, in the history of old and new. We find it in the delightful myth of Antheus, who drives power from the earth; we find it among the subtle speculations of one of your splendid mathematicians, and in many hints and statements of thinkers of the present time. Throughout space there is energy. Is this energy static or kinetic? If static, our hopes are in vain; if kinetic - and this we know it is for certain - then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.

Experiments With Alternate Currents Of High Potential And High Frequency (February 1892).

Close